Regularization: Bias Variance Tradeoff, l2 regularization, Early stopping, Dataset augmentation, Parameter sharing and tying, Injecting noise at input, Ensemble methods, Dropout
Mitesh M. Khapra
CS7015 (Deep Learning) : Lecture 6


AI4Bharat, Department of Computer
Science and Engineering, IIT Madras
References/Acknowledgments
So far, we have focused on minimizing the objective function using a variety of optimization algorithms
Deep learning models typically have BILLIONS of parameters whereas the training data may have only MILLIONS of samples
Therefore, they are called over-parameterized models
Over-parameterized models are prone to a phenomenon called over-fitting
To understand this, let's start with bias and variance of a model with respect to its capacity
The Problem
Module 6.1 : Bias and Variance
Mitesh M. Khapra


AI4Bharat, Department of Computer
Science and Engineering, IIT Madras
We will begin with a quick overview of bias, variance and the trade-off between them.
Let us consider the problem of fitting a curve through a given set of points
We consider two models :
\(Simple \)
(\(degree:1\))
\(y = \hat {f}(x) = w_1x +w_0\)
\(Complex \)
(\(degree:25\))
Note that in both cases we are making an assumption about how \(y\) is related to \(x\). We have no idea about the true relation \(f(x)\)
The points were drawn from a sinusoidal function (the true \(f(x)\))
The training data consists of 500 points
\(y = \hat {f}(x) = \displaystyle \sum_{i=1}^{25} w_i x^i+w_0\)
We sampled 500 points from the training data and train a simple and a complex model
We repeat the process ‘k’ times to train multiple models (each model sees a different sample of the training data)
We make a few observations from these plots
The points were drawn from a sinusoidal function (the true \(f(x)\))
Simple models trained on different samples of the data do not differ much from each other
However they are very far from the true sinusoidal curve (under fitting)
On the other hand, complex models trained on different samples of the data are very different from each other (high variance)
Let \(f(x)\) be the true model (sinusoidal in this case) and \(\hat {f}(x)\) be our estimate of the model (simple or complex, in this case) then,
Bias \(\hat {f}(x)\) \(= E\) [\(\hat {f}(x)\)] \(- f(x)\)
Green Line: Average value of \(\hat {f}(x)\)for the simple model
Blue Curve: Average value of \(\hat {f}(x)\) for the complex model
Red Curve: True model (\(f(x))\)
\(E\) [\(\hat {f}(x)\)] is the average (or expected) value of the model
We can see that for the simple model the average value (green line) is very far from the true value \(f(x)\) (sinusoidal function)
Mathematically, this means that the simple model has a high bias
On the other hand, the complex model has a low bias

We now define,
Variance \(\hat{f}(x) = E\bigg[(\hat{f}(x) - E[\hat{f}(x)])^2\bigg]\) (Standard definition from statistics)
Roughly speaking it tells us how much the different \(\hat {f}(x)\)’s (trained on different samples of the data) differ from each other)
It is clear that the simple model has a low variance whereas the complex model has a high variance

In summary (informally)
Simple model: high bias, low variance
Complex model: low bias, high variance
There is always a trade-off between the bias and variance
Both bias and variance contribute to the mean square error. Let us see how


Module 6.2 : Train error vs Test error
Mitesh M. Khapra


AI4Bharat, Department of Computer
Science and Engineering, IIT Madras
Consider a new point (\(x, y)\) which was not seen during training
If we use the model \(\hat {f}(x)\) to predict the value of \(y\) then the mean square error is given by
\(E[(y −\) \(\hat {f}(x))^2 ]\)
(average square error in predicting \(y\) for many such unseen points)
We can show that
\(E[(y −\) \(\hat {f}(x))^2 \)] \(= Bias^2\)
\(+ Variance\)
\(+ \sigma^2\) (irreducible error)
The parameters of \(\hat {f}(x)\) (all \(w_i\) ’s) are trained using a training set \(\{(x_i , y_i)\} ^n_ {i=1}\)
However, at test time we are interested in evaluating the model on a validation (unseen) set which was not used for training
This gives rise to the following two entities of interest:
\(train_{err}\) (say, mean square error)
\(test_{err}\) (say, mean square error)
Typically these errors exhibit the trend shown in the adjacent figure
\(E[(y −\) \(\hat {f}(x))^2 \)] \(= Bias^2\)
\(+ Variance\)
\(+ \sigma^2\) (irreducible error)
error
model complexity
High bias
High variance
Sweet spot-
-perfect tradeoff
-ideal model
complexity


Let there be \(n\) training points and \(m\) test (validation) points
Intuitions developed so far
\(train_{err}\) = \(\frac {1}{n} \displaystyle \sum_{i=1}^n (y_{i} - \hat f {(x_i)})^2\)
\(test_{err} =\) \(\frac {1}{m} \displaystyle \sum_{i=n+1}^{n+m} (y_{i} - \hat f {(x_i)})^2\)
As the model complexity increases \(train_{err}\) becomes overly optimistic and gives us a wrong picture of how close \(\hat f\) is to \(f\)
The validation error gives the real picture of how close \(\hat f\) is to \(f\)
We will concretize this intuition mathematically now and eventually show how to account for the optimism in the training error
Let D=\({\{x_i , y_i\}} ^{m+n}_ {i=1}\)
We know that some true function exists, s.t.,
\(y = f(x) + ε\)
which means that \(y_i\) is related to \(x_i\) by some true function \(f\) but there is also some noise \(ε\) in the relation
For simplicity, we assume
\(ε ∼ N (0, σ^2 )\)
and of course we do not know \(f\)
Further we use \(\hat f\) to approximate \(f\) and estimate the parameters using T \(\subset\) D such that
\(y = \hat f(x)\)
We are interested in knowing
\(E[( \hat f(x) − f(x))^2 ]\)
but we cannot estimate this directly because we do not know \(f\)
We will see how to estimate this empirically using the observation \(y_i\) & prediction \(\hat y_i\)
\(E[( \hat y − y)^ 2 ]\)
\(= E[( \hat f(x) − f(x) − ε)^ 2 ]\) (\(y = f(x) + ε)\)
\(= E[( \hat f(x) − f(x))^2 − 2ε( \hat f(x) − f(x)) + ε^2 ]\)
\(= E[( \hat f(x) − f(x))^2 ] − 2E[ε( \hat f(x) − f(x))] + E[ε^2 ]\)
\(∴ E[( \hat f(x) − f(x))^2 ] = E[( \hat y − y)^2 ] − E[ε^2 ] + 2E[ ε( \hat f(x) − f(x)) ]\)
\(E[( \hat y_i − y_i)^ 2 ]\)
\(= E[( \hat f(x_i) − f(x_i) − ε_i)^ 2 ]\) (\(y_i = f(x_i) + ε_i)\)
\(= E[( \hat f(x_i) − f(x_i))^2 − 2ε_i( \hat f(x_i) − f(x_i)) + ε^2_i ]\)
\(= E[( \hat f(x_i) − f(x_i))^2 ] − 2E[ε_i( \hat f(x_i) − f(x_i))] + E[ε^2_i ]\)
\(∴ E[( \hat f(x_i) − f(x_i))^2 ] = E[( \hat y_i − y_i)^2 ] − E[ε^2_i ] + 2E[ ε_i( \hat f(x_i) − f(x_i)) ]\)
We will take a small detour to understand how to empirically estimate an Expectation and then return to our derivation
Suppose we have observed the goals scored (\(z)\) in \(k\) matches as
\(z_1\) = 2, \(z_2\) = 1, \(z_3\) = 0, ... \(z_k\) = 2
Now we can empirically estimate \(E[z]\) i.e. the expected number of goals scored as
\(E[z] = \frac {1}{k} \displaystyle \sum_{i=1}^k z_i\)
Analogy with our derivation: We have a certain number of observations \(y_i\) & predictions \(\hat y_i\) using which we can estimate
\(E[( \hat y − y)^2 ] =\)
\(\frac {1}{m} \displaystyle \sum_{i=1}^m (\hat y_i - y_i)^2\)
... returning back to our derivation
\(E[( \hat f(x) − f(x))^2 ] = E[( \hat y − y)^2 ] − E[ε^2] + 2E[ ε( \hat f(x) − f(x)) ]\)
We can empirically evaluate R.H.S using training observations or test observations
Case 1: Using test observations
\(\underbrace {E[( \hat f(x) − f(x))^2 ]}_{true \space error} \)
\(= \underbrace {\frac{1}{m} \displaystyle \sum_{i=n+1}^{n+m} (\hat y_i - y_{i}) ^2}_ {empirical \space estimation \space of \space error} -\)
\(\underbrace {\sigma^2 }_ {small \space constant} +\)
\(\underbrace{2 E[ ε( \hat f(x) − f(x))]}_ {= \space covariance (\space ε, ( \hat f(x) − f(x))}\)
\(∵\) covariance \((X, Y )\)
\(= E[(X − \mu_X)(Y − \mu_Y )]\)
\(= E[(X)(Y − \mu_Y )](\)if \(\mu_X = E[X] = 0)\)
\(= E[XY ] − E[X{\mu_Y}]\)
\(= E[XY ] − \mu_Y E[X]\)
\(= E[XY ]\)
\(\underbrace {E[( \hat f(x) − f(x))^2 ]}_{true \space error} \)
\(= \underbrace {\frac{1}{m} \displaystyle \sum_{i=n+1}^{n+m} (\hat y_i - y_{i}) ^2}_ {empirical \space estimation \space of \space error} -\)
\(\underbrace {\sigma^2 }_ {small \space constant} +\)
\(\underbrace{2 E[ ε( \hat f(x) − f(x))]}_ {= \space covariance \space( ε, \hat f(x) − f(x))}\)
None of the test observations participated in the estimation of \(\hat f(x)\) [the parameters of \(\hat f(x)\) were estimated only using training data]
\(\because ε = ( y − f(x))\)
\(∴ E[ε\space · ( \hat f(x) − f(x))]\)
\(= E[ε ] · E[ \hat f(x) − f(x))]\)
\(= 0 \space · \space E[ \hat f(x) − f(x))]\)
\(= 0\)
∴ true error = empirical test error + small constant
Hence, we should always use a validation set(independent of the training set) to estimate the error M
\(∴ ε ⊥ ( \hat f(x) − f(x))\)
\(∴ (y - f(x) )⊥ ( \hat f(x) − f(x))\)
Case 2: Using training observations
\(\underbrace {E[( \hat f(x) − f(x))^2 ]}_{true \space error} \)
\(= \underbrace {\frac{1}{n} \displaystyle \sum_{i=1}^{n} (\hat y_i - y_{i}) ^2}_ {empirical \space estimation \space of \space error} -\)
\(\underbrace {\sigma^2 }_ {small \space constant} +\)
\(\underbrace{2 E[ ε( \hat f(x) − f(x))]}_ {= \space covariance \space( ε \hat f(x) − f(x))}\)
Now, \(y-f(x) \space \cancel{⊥} \space \hat f(x) - f(x)\) because the training data was used for estimating the parameters of \(\hat f(x)\)
\(\cancel{=} \space E[ε ] \space·\space E[ \hat f(x) − f(x))]\)
Hence, the empirical train error is smaller than the true error and does not give a true picture of the error
But how is this related to model complexity? Let us see
\(\cancel{=} \space 0\)
\(\space E[ε · \hat f(x) − f(x))]\)
Module 6.3 : True error and Model complexity
Mitesh M. Khapra


AI4Bharat, Department of Computer
Science and Engineering, IIT Madras
Using Stein’s Lemma (and some trickery) we can show that
\(\frac{1}{n} \displaystyle \sum_{i=1}^{n} ε_i( \hat f(x_i) − f(x_i)) = \frac {\sigma^2}{n}\displaystyle \sum_{i=1}^{n} \frac{∂ \hat f(x_i)} {∂y_i}\)
When will \( \frac{∂ \hat f(x_i)} {∂y_i}\) be high? When a small change in the observation causes a large change in the estimation(\(\hat f\))
Can you link this to model complexity?
Yes, indeed a complex model will be more sensitive to changes in observations whereas a simple model will be less sensitive to changes in observations
Hence, we can say that true error \(=\) empirical train error \(+\) small constant \(+\) \(Ω\)(model complexity)
\( E[ ε( \hat f(x) − f(x))] \)
Let us verify that indeed a complex model is more sensitive to minor changes in the data
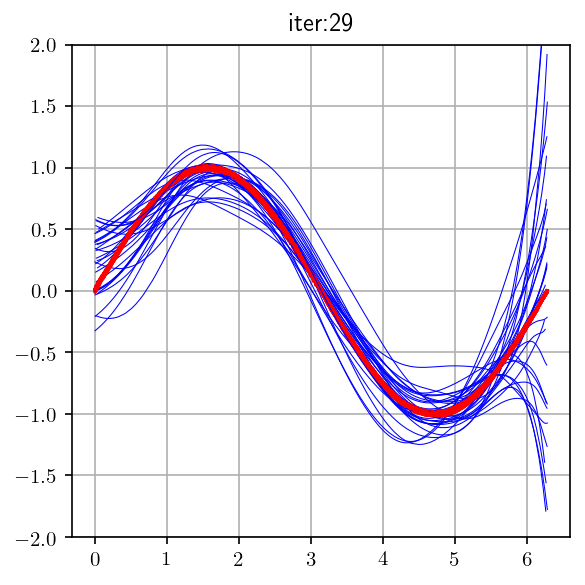
We have fitted a simple and complex model for some given data
We now change one of these data points

Let us verify that indeed a complex model is more sensitive to minor changes in the data
We have fitted a simple and complex model for some given data
We now change one of these data points
The simple model does not change much as compared to the complex model

Hence while training, instead of minimizing the training error \(\mathscr {L}_{train} (\theta)\) we should minimize
min\(_{w.r.t \space \theta}\) \(\space \mathscr {L}_{train} (\theta)+ Ω(θ) = \mathscr {L}(\theta)\)
Where \(Ω(\theta)\) would be high for complex models and small for simple models
\(Ω(\theta)\) acts as an approximate for \(\frac {\sigma^2}{n}\textstyle \sum_{i=1}^{n} \frac{∂ \hat f(x_i)} {∂y_i}\)
This is the basis for all regularization methods
We can show that \(l_1\) regularization, \(l_2\) regularization, early stopping and injecting noise in input are all instances of this form of regularization.
error
model complexity
High bias
High variance
Sweet spot


\(Ω(\theta)\) should ensure that model has reasonable complexity

Why do we care about this bias variance tradeoff and model complexity?
Deep Neural networks are highly complex models.
Many parameters, many non-linearities.
It is easy for them to overfit and drive training error to 0.
Hence we need some form of regularization.
\(l_2\) regularization
Dataset augmentation
Parameter Sharing and tying
Adding Noise to the inputs
Adding Noise to the outputs
Early stopping
Ensemble methods
Dropout
Different forms of regularization
Module 6.4 : \(l_2\) regularization
Mitesh M. Khapra


AI4Bharat, Department of Computer
Science and Engineering, IIT Madras
Different forms of regularization
\(l_2\) regularization
Dataset augmentation
Parameter Sharing and tying
Adding Noise to the inputs
Adding Noise to the outputs
Early stopping
Ensemble methods
Dropout
For \(l_2\) regularization we have,
\(\widetilde{\mathscr {L}}(w) = \mathscr {L}(w) + \frac{\alpha}{2}\|w\|^2 \)
For SGD (or its variants), we are interested in
\(\nabla \widetilde{\mathscr {L}}(w) = \nabla \mathscr {L}(w) + \alpha w \)
Update rule:
\(w_{t+1} = w_t - \eta \nabla \mathscr {L}(w_t) - \eta \alpha w_t \)
Requires a very small modification to the code
Let us see the geometric interpretation of this
Assume \(w^∗\) is the optimal solution for \(\mathscr {L}(w)\) [not \(\widetilde{ \mathscr {L}}(w)\)] i.e. the solution in the absence of regularization (\(w^∗\) optimal → \(\nabla \mathscr {L}(w^*)=\) 0)
Consider \(u = w − w^∗\) . Using Taylor series approximation (upto \(2^{nd}\) order)
\(\mathscr {L}(w^* + u) = \mathscr {L}(w^*) + u^T \nabla \mathscr {L}(w^*) + \dfrac{1}{2}u^THu\)
\(\mathscr {L}(w) = \mathscr {L}(w^*) + (w - w^*)^T \nabla \mathscr {L}(w^*) + \dfrac{1}{2}(w - w^*)^TH(w - w^*)\)
\(= \mathscr {L}(w^*) + \dfrac{1}{2}(w - w^*)^TH(w - w^*)\) \((∵ \nabla \mathscr {L}(w^*) = 0)\)
\(\nabla \mathscr {L}(w)= \nabla \mathscr {L}(w^*) + H(w - w^*)\)
\(= H(w - w^*)\)
Now,
\(\nabla \widetilde{\mathscr {L}}(w) = \nabla \mathscr{L}(w) + \alpha w\)
\(= H(w - w^*) + \alpha w\)
Let \(\widetilde w\) be the optimal solution for \(\widetilde{\mathscr{L}}(w)\) [i.e regularized loss]
\(∵ \nabla \widetilde{\mathscr {L}}(\widetilde w) = 0\)
\(H( \widetilde{w} - w^*) + \alpha \widetilde w = 0\)
\(∴ (H + \alpha \mathbb I) \widetilde{w} = H w^* \)
\(∴ \widetilde w = (H + \alpha \mathbb I)^{-1} H w^* \)
Notice that if \(\alpha → 0\) then \(\widetilde w → w^∗\) [no regularization]
But we are interested in the case when \(\alpha \space \cancel{=} \space 0\)
Let us analyse the case when \(\alpha \space \cancel{=} \space 0\)
If H is symmetric Positive Semi Definite
\(H = Q \Lambda Q^T\) [\(Q\) is orthogonal, \(QQ^T = Q^TQ = \mathbb I\)]
\(∴ \widetilde w = (H + \alpha \mathbb I)^{-1} H w^* \)
\(= (Q \Lambda Q^T + \alpha \mathbb I)^{-1} Q \Lambda Q^T w^*\)
\(= (Q \Lambda Q^T + \alpha Q \mathbb I Q^T)^{-1} Q \Lambda Q^T w^*\)
\(= [Q (\Lambda+ \alpha \mathbb I) Q^T]^{-1} Q \Lambda Q^T w^*\)
\(= Q^{T^{-1}} (\Lambda+ \alpha \mathbb I)^{-1} Q^{-1} Q \Lambda Q^T w^*\)
\(= Q (\Lambda+ \alpha \mathbb I)^{-1} \Lambda Q^T w^*\) (\(∵ Q^{T^{-1}} = Q\))
\(∴ \widetilde w = (QDQ)^{T} w^* \)
where \(D = (\Lambda + \alpha \mathbb I)^{−1} \Lambda\), is a diagonal matrix which we will see in more detail soon
\(∴ \widetilde w = Q(\Lambda + \alpha \mathbb I)^{−1} \Lambda Q^T w^* \)
\(= QDQ^T w^* \)
So what is happening here?
\(w^∗\) first gets rotated by \(Q^T\) to give \(Q^T w^∗\)
However if \(\alpha = 0\) then \(Q\) rotates \(Q^T w^∗\) back to give \(w^∗\)
If \(\alpha \space \cancel{=} \space 0\) then let us see what \(D\) looks like
\((\Lambda + \alpha \mathbb I)^{−1} =\)
\(D = (\Lambda + \alpha \mathbb I)^{−1} \Lambda\)
\((\Lambda + \alpha \mathbb I)^{−1} \Lambda =\)
So what is happening now?
\(∴ \widetilde w = Q(\Lambda + \alpha \mathbb I)^{−1} \Lambda Q^T w^* \)
\(= QDQ^T w^* \)
Each element \(i\) of \(Q^T w^∗\) gets scaled by \(\frac {\lambda_i} {\lambda_i + a}\) before it is rotated back by \(Q\)
if \(\lambda_i >> \alpha\) then \(\frac {\lambda_i} {\lambda_i + a} = 1\)
if \(\lambda_i << \alpha\) then \(\frac {\lambda_i} {\lambda_i + a} = 0\)
Thus only significant directions (larger eigen values) will be retained.
\((\Lambda + \alpha \mathbb I)^{−1} =\)
\(D = (\Lambda + \alpha \mathbb I)^{−1} \Lambda\)
\((\Lambda + \alpha \mathbb I)^{−1} \Lambda =\)
Effective parameters \( = \displaystyle \sum_{i=1}^{n} \frac{\lambda_i}{\lambda_i + a} < n \)
The weight vector\((w^∗)\) is getting rotated to (\(\widetilde w)\)
All of its elements are shrinking but some are shrinking more than the others
This ensures that only important features are given high weights

\(w_1\)
\(w_2\)

\(\tilde w\)
\(w^*\)
Module 8.5 : Dataset augmentation
Mitesh M. Khapra


AI4Bharat, Department of Computer
Science and Engineering, IIT Madras
\(l_2\) regularization
Dataset augmentation
Parameter Sharing and tying
Adding Noise to the inputs
Adding Noise to the outputs
Early stopping
Ensemble methods
Dropout
Different forms of regularization
[given training data]
label = 2
[augmented data = created using some knowledge of the
task]
We exploit the fact that
certain transformations
to the image do not
change the label of the
image.

rotated by \(20\degree\)

rotated by \(65\degree\)

shifted vertically

shifted horizontally

blurred

changed some pixels
label = 2

Typically, More data \(=\) better learning
Works well for image classification / object recognition tasks
Also shown to work well for speech
For some tasks it may not be clear how to generate such data
Module 6.6 : Parameter Sharing and tying
Mitesh M. Khapra


AI4Bharat, Department of Computer
Science and Engineering, IIT Madras
\(l_2\) regularization
Dataset augmentation
Parameter Sharing and tying
Adding Noise to the inputs
Adding Noise to the outputs
Early stopping
Ensemble methods
Dropout
Other forms of regularization
Used in CNNs
Same filter applied at different positions of the image
Or same weight matrix acts on different input neurons
\(\hat x\)
\(h( x)\)
\( x\)
Typically used in autoencoders.
The encoder and decoder weights are tied.
Parameter Sharing
Parameter Tying

Module 6.7 : Adding Noise to the inputs
Mitesh M. Khapra


AI4Bharat, Department of Computer
Science and Engineering, IIT Madras
\(l_2\) regularization
Dataset augmentation
Parameter Sharing and tying
Adding Noise to the inputs
Adding Noise to the outputs
Early stopping
Ensemble methods
Dropout
Other forms of regularization
\(\hat x\)
\(h( x)\)
\(\widetilde x\)
\(P(\widetilde x \mid x)←noise \space process\)
\( x\)
We saw this in Autoencoder
We can show that for a simple input output neural network, adding Gaussian noise to the input is equivalent to weight decay (L2 regularisation)
Can be viewed as data augmentation
\(ε ∼ N (0, \sigma^2 )\)
\(\widetilde {x}_i = x_i + ε_i\)
\(\widehat y = \displaystyle \sum_{i=1}^{n} w_i x_i\)
\(= \displaystyle \sum_{i=1}^{n} w_i x_i + \displaystyle \sum_{i=1}^{n} w_i ε_i\)
\(= \widehat y + \displaystyle \sum_{i=1}^{n} w_i ε_i\)
We are interested in \(E[(\widetilde y - y)^2]\)
\(E[(\widetilde y - y)^2] = E \Biggl [(\hat y + \displaystyle \sum_{i=1}^{n} w_i ε_i -y)^2 \Biggl] \)
\(= E \Biggl [\bigg(\big(\hat y - y \big) + \big(\displaystyle \sum_{i=1}^{n} w_i ε_i )\bigg)^2 \Biggl] \)
\(= E [(\hat y - y)^2] + E \Big[2(\hat y - y) \displaystyle \sum_{i=1}^{n} w_i ε_i\Big] + E \Big[ \big(\displaystyle \sum_{i=1}^{n} w_i ε_i \big)^2 \Big] \)
\(= E [(\hat y - y)^2] + 0 + E \Big[ \displaystyle \sum_{i=1}^{n} {w_i}^2 {ε_i}^2 \Big] \)
(\(∵ ε_i\) is independent of \(ε_j\) and \(ε_i\) is independent of \((\hat y-y)\))
\(= (E \Big[(\hat y - y)^2\Big] + \sigma^2 \displaystyle \sum_{i=1}^{n} {w_i}^2\) (same as \(L_2\) norm penalty)
\(\tilde y = \displaystyle \sum_{i=1}^{n} w_i \widetilde{x}_i\)
\(x_1 + ε_1\)
\(x_2 + ε_2\)
\(x_k + ε_k\)
\(x_n + ε_n\)
Module 6.8 : Adding Noise to the outputs
Mitesh M. Khapra


AI4Bharat, Department of Computer
Science and Engineering, IIT Madras
\(l_2\) regularization
Dataset augmentation
Parameter Sharing and tying
Adding Noise to the inputs
Adding Noise to the outputs
Early stopping
Ensemble methods
Dropout
Other forms of regularization
minimize : \( \displaystyle \sum_{i=0}^{9} p_i \space log \space q_i\)
true distribution : \(p = {0, 0, 1, 0, 0, 0, 0, 0, 0, 0}\)
estimated distribution : \(q\)
Intuition
Do not trust the true labels, they may be noisy
Instead, use soft targets
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
Hard Targets

\(ε =\) small positive constant
minimize : \( \displaystyle \sum_{i=0}^{9} p_i \space log \space q_i\)
true distribution + noise : \(p =\{\frac{\varepsilon}{9}, \frac{\varepsilon}{9}, 1 - \varepsilon, \frac{\varepsilon}{9}, ... \} \)
estimated distribution : \(q\)
Soft Targets

\(\frac{ε}{9}\)
\(\frac{ε}{9}\)
\(\frac{ε}{9}\)
\(\frac{ε}{9}\)
\(\frac{ε}{9}\)
\(\frac{ε}{9}\)
\(\frac{ε}{9}\)
\(\frac{ε}{9}\)
\(\frac{ε}{9}\)
\(1-ε\)
Module 6.9 : Early stopping
Mitesh M. Khapra


AI4Bharat, Department of Computer
Science and Engineering, IIT Madras
\(l_2\) regularization
Dataset augmentation
Parameter Sharing and tying
Adding Noise to the inputs
Adding Noise to the outputs
Early stopping
Ensemble methods
Dropout
Other forms of regularization
Track the validation error
Have a patience parameter \(p\)
If you are at step \(k\) and there was no improvement in validation error in the previous \(p\) steps then stop training and return the model stored at step \(k − p\)
Basically, stop the training early before it drives the training error to 0 and blows up the validation error
\(\text{Error}\)
\(\text {Steps}\)
\(Validation \) \(error\)
\(Training\) \(error\)

\(k-p\)
\(return\) \(this\) \(model\)
\(k\)
\(stop\)
Very effective and the mostly widely used form of regularization
Can be used even with other regularizers (such as \(l_2\))
How does it act as a regularizer ?
We will first see an intuitive explanation and then a mathematical analysis
\(\text{Error}\)
\(\text {Steps}\)
\(Validation \) \(error\)
\(Training\) \(error\)

\(k-p\)
\(return\) \(this\) \(model\)
\(k\)
\(stop\)
Recall that the update rule in SGD is
\(w_{t+1} = w_t - \eta \nabla w_t\)
\(= w_0 - \eta \displaystyle \sum_{i=1}^{t} \nabla w_i \)
Let \(τ\) be the maximum value of \( \nabla w_i\) then
\(\mid w_{t+1} - w_0 \mid \space \leq \eta t \mid τ \mid\)
Thus, \(t\) controls how far \(w_t\) can go from the initial \(w_0\)
In other words it controls the space of exploration
\(\text{Error}\)
\(\text {Steps}\)
\(Validation \) \(error\)
\(Training\) \(error\)

\(k-p\)
\(return\) \(this\) \(model\)
\(k\)
\(stop\)
We will now see a mathematical analysis of this
Recall that the Taylor series approximation for \(\mathscr{L} (w)\) is
\(\mathscr{L}(w) = \mathscr{L}(w^*) + (w - w^*)^T \nabla \mathscr{L}(w^*) + \dfrac{1}{2} (w - w^*)^T H(w - w^*) \)
\(= \mathscr{L}(w^*) + \dfrac{1}{2} (w - w^*)^T H(w - w^*) \) \([ w^* \space is \space optimal \space so \space \nabla \mathscr{L} (w^∗) \space is \space 0 ]\)
\( \nabla (\mathscr{L} (w^∗))= H(w - w^*) \)
Now the SGD update rule is:
\(w_t = w_{t-1} - \eta \nabla \mathscr{L} (w_{t-1})\)
\(= w_{t-1} - \eta H (w_{t-1} - w^*)\)
\(= (I - \eta H)w_{t-1} + \eta H w^*\)
\(w_t = (I - \eta H)w_{t-1} + \eta H w^*\)
Using EVD of \(H\) as \(H\) = \(Q \Lambda Q^T\) , we get:
\(w_t = (I - \eta Q \Lambda Q^T)w_{t-1} + \eta Q \Lambda Q^T w^*\)
If we start with \(w_0 = 0\) then we can show that (See Appendix)
\(w_t = Q[I - (I - \varepsilon \Lambda)^t] Q^T w^*\)
Compare this with the expression we had for optimum \(\tilde W\) with \(L_2\) regularization
\(\tilde w = Q[I - (\Lambda + \alpha I)^{-1} \alpha] Q^T w^*\)
We observe that \(w_t = \tilde w\), if we choose \(ε,t\) and \(\alpha\) such that
\((I - \varepsilon \Lambda)^t = (\Lambda + \alpha I)^{-1} \alpha \)
Early stopping only allows \(t\) updates to the parameters.
If a parameter \(w\) corresponds to a dimension which is important for the loss \(\mathscr{L} (\theta)\) then \(\frac {∂\mathscr{L} (\theta)}{∂w}\) will be large
However if a parameter is not important (\(\frac {∂\mathscr{L} (\theta)}{∂w}\) is small) then its updates will be small and the parameter will not be able to grow large in '\(t\)' steps
Early stopping will thus effectively shrink the parameters corresponding to less important directions (same as weight decay).
Things to be remember
Module 6.10 : Ensemble methods
Mitesh M. Khapra


AI4Bharat, Department of Computer
Science and Engineering, IIT Madras
\(l_2\) regularization
Dataset augmentation
Parameter Sharing and tying
Adding Noise to the inputs
Adding Noise to the outputs
Early stopping
Ensemble methods
Dropout
Other forms of regularization
Combine the output of different models to reduce generalization error
The models can correspond to different classifiers
It could be different instances of the same classifier trained with:
different hyperparameters
different features
different samples of the training data
\(y_{final}\)
\(y_{lr}\)
\(y_{nb}\)
\(y\)
\(y\)
\(y_{svm}\)
\(x_1\)
\(x_2\)
\(x_3\)
\(x_4\)
\(Logistic Regression\)
\(SVM\)
\(Naive Bayes\)
Bagging: form an ensemble using different instances of the same classifier
From a given dataset, construct multiple training sets by sampling with replacement \((T_1, T_2, ..., T_k)\)
Train \(i^{th}\) instance of the classifier using training set \(T_i\)
Each model trained with a different sample of the data (sampling with replacement)
\(y_{final}\)
\(y_{lr1}\)
\(y_{lr3}\)
\(y\)
\(y\)
\(y_{lr2}\)
\(y\)
\(Logistic \)
\(Regression\)
\(Logistic \)
\(Regression\)
\(Logistic \)
\(Regression\)
When would bagging work?
Consider a set of k LR models
Suppose that each model makes an error \(\varepsilon_i\) on a test example
The error made by the average prediction of all the models is \(\frac {1}{k} \textstyle \sum_{i} \varepsilon_i\)
Let \(\varepsilon_i\) be drawn from a zero mean multivariate normal distribution
\(Variance = E[\varepsilon_i^2] = V\)
\(Covariance = E[\varepsilon_i \varepsilon_j] = C\)
The expected squared error is :
\(mse = E[(\frac {1}{k} \textstyle \sum_{i} \varepsilon_i)^2]\)
\(= \frac {1}{k^2} E[ \displaystyle \sum_{i} \displaystyle \sum_{i = j} \varepsilon_i \varepsilon_j + \displaystyle \sum_{i} \displaystyle \sum_{i \cancel{=} j} \varepsilon_i \varepsilon_j ]\)
\(= \frac {1}{k^2} E[ \displaystyle \sum_{i} \varepsilon_i^2 + \displaystyle \sum_{i} \displaystyle \sum_{i \cancel{=} j} \varepsilon_i \varepsilon_j ]\)
\(= \frac {1}{k^2} (\displaystyle \sum_{i} E [\varepsilon_i^2] + \displaystyle \sum_{i} \displaystyle \sum_{i \cancel{=} j} E[\varepsilon_i \varepsilon_j ])\)
\(= \frac {1}{k^2} (kV+ k(k-1)C)\)
\(= \frac {1}{k}V + \dfrac{k-1}{k}C\)
When would bagging work?
If the errors of the model are perfectly correlated then \(V = C\) and \(mse = V\) [bagging does not help: the mse of the ensemble is as bad as the individual models]
If the errors of the model are independent or uncorrelated then \(C = 0\) and the mse of the ensemble reduces to \(\frac{1}{k}V\)
\(mse = \frac {1}{k}V + \dfrac{k-1}{k}C\)
On average, the ensemble will perform at least as well as its individual members
Module 6.11 : Dropout
Mitesh M. Khapra


AI4Bharat, Department of Computer
Science and Engineering, IIT Madras
\(l_2\) regularization
Dataset augmentation
Parameter Sharing and tying
Adding Noise to the inputs
Adding Noise to the outputs
Early stopping
Ensemble methods
Dropout
Other forms of regularization
Typically model averaging (bagging ensemble) always helps
Training several large neural networks for making an ensemble is prohibitively expensive
Option 1: Train several neural networks having different architectures(obviously expensive)
Option 2: Train multiple instances of the same network using different training samples (again expensive)
Even if we manage to train with option 1 or option 2, combining several models at test time is infeasible in real time applications
Dropout is a technique which addresses both these issues.
Effectively it allows training several neural networks without any significant computational overhead.
Also gives an efficient approximate way of combining exponentially many different neural networks.
Dropout refers to dropping out units
Temporarily remove a node and all its incoming/outgoing connections resulting in a thinned network
Each node is retained with a fixed probability (typically \(p = 0.5\)) for hidden nodes and \(p = 0.8\) for visible nodes
Suppose a neural network has \(n\) nodes
Using the dropout idea, each node can be retained or dropped
Of course, this is prohibitively large and we cannot possibly train so many networks
For example, in the above case we drop \(5\) nodes to get a thinned network
Given a total of \(n\) nodes, what are the total number of thinned networks that can be formed?
Trick: (1) Share the weights across all the networks
\(2^n\)
(2) Sample a different network for each training instance
Let us see how?
We initialize all the parameters (weights) of the network and start training
For the first training instance (or mini-batch), we apply dropout resulting in the thinned network
Which parameters will we update?
We compute the loss and backpropagate
Only those which are active
We initialize all the parameters (weights) of the network and start training
For the first training instance (or mini-batch), we apply dropout resulting in the thinned network
Which parameters will we update?
We compute the loss and backpropagate
Only those which are active
We initialize all the parameters (weights) of the network and start training
For the first training instance (or mini-batch), we apply dropout resulting in the thinned network
Which parameters will we update?
We compute the loss and backpropagate
Only those which are active
We initialize all the parameters (weights) of the network and start training
For the first training instance (or mini-batch), we apply dropout resulting in the thinned network
Which parameters will we update?
We compute the loss and backpropagate
Only those which are active
For the second training instance (or mini-batch), we again apply dropout resulting in a different thinned network
We again compute the loss and backpropagate to the active weights
For the second training instance (or mini-batch), we again apply dropout resulting in a different thinned network
If the weight was active for only one of the training instances then it would have received only one updates by now
Each thinned network gets trained rarely (or even never) but the parameter sharing ensures that no model has untrained or poorly trained parameters
We again compute the loss and backpropagate to the active weights
If the weight was active for both the training instances then it would have received two updates by now
What happens at test time?
Impossible to aggregate the outputs of \(2^n\) thinned networks
Instead we use the full Neural Network and scale the output of each node by the fraction of times it was on during training
Present with probability \(p\)
\(w_1\)
\(w_2\)
\(w_3\)
\(w_4\)
At training time
Always
present
\(pw_1\)
\(pw_2\)
\(pw_3\)
\(pw_4\)
At test time
Dropout essentially applies a masking noise to the hidden units
Prevents hidden units from coadapting
Essentially a hidden unit cannot rely too much on other units as they may get dropped out any time
Each hidden unit has to learn to be more robust to these random dropouts
Here is an example of how dropout helps in ensuring redundancy and robustness
Suppose \(h_i\) learns to detect a face by firing on detecting a nose
Dropping \(h_i\) then corresponds to erasing the information that a nose exists
The model should then learn another \(h_i\) which redundantly encodes the presence of a nose
Or the model should learn to detect the face using other features
\(h_i\)
Visualizing the loss surface of deep network* before and after applying regularization
*There are computationally intensive techniques which allow us to visualize the loss landscape of deep networks either in 1-D or 2-D. For more, refer to this paper
The loss landscape
Feel free to play with the loss landscape : https://losslandscape.com/explorer

Researchers have correlated the local flatness (curvature) of the loss surface to the generalization of a model with different measures of curvature
Flat surface \(\rightarrow\) better generalization
Sharp surface \(\rightarrow\) poor generalization
It has been shown that explicit regularization techniques smoothen the loss surface

Module 6.12 : Implicit Regularization
Mitesh M. Khapra


AI4Bharat, Department of Computer Science and Engineering, IIT Madras
Grouping Regularization Techniques
Data \(x_i\)
1. Data Augmentation
2. Noise Injection
Architecture choice \(f(\cdot)\)
1. Dropout
2. Skip connections (CNN)
3. Weight sharing
4. Pooling
Penalize cost \(\mathscr{L}(\cdot)\)
1. \(L_1\)
2. \(L_2\)
Optimizer \(\nabla\)
1. SGD
2. Early stopping
Grouping Regularization Techniques
Explicit
Data Augmentation
Noise Injection
Dropout
Skip connections (CNN)
Weight sharing
Pooling
Implicit
\(L_1\), \(L_2\)
SGD
Large initial learning rate
Small initial learning rate
Early stopping
Is using regularization technique (adopted from statistical learning theory) really the fundamental reason to obtain better generalization of deep learning models?
Is using regularization technique (adopted from statistical learning theory) really the fundamental reason to obtain better generalization of deep learning models?
Let's find out
Random Labelling : paper
Suppose that we replace the true labels of training data by some random labels
Let's consider a deep neural net that performed well on some task (say, classification) and fix its complexity (that is, size of network and hence number of parameters), optimizer used to train the model, initialization..
By doing so, we remove relations (regularity) between inputs and corresponding outputs.
Let's try to answer this with a simple (and toy) example that we have already used in the beginning of the lecture
What is the consequence then?

The plot on the left shows some data points sampled from a noisy sinusoid.
Suppose that we use a model with the complexity of 19 (i.e, 19 parameters)
After training the model, the model fits the data points and closely represents the true function

What happens if we randomly shuffle \(y\)?
Does the model (with its fixed capacity) fit the data?
Let's see
This behaviour is expected!
Because, by shuffling \(y\), we remove the regularity (relation) in the data points.
Therefore, the training error remains high!
Do deep neural nets behave the same way?
Surprisingly, No! They drive the training error to zero with random labelling (which removes the relation between samples and labels)!

Note, however, random labels are fixed and consistent across epochs
The observation
..observations on both explicit and implicit regularizers are consistently suggesting that regularizers, when properly tuned, could help to improve the generalization performance.
However, it is unlikely that the regularizers are the fundamental reason for generalization, as the networks continue to perform well after all the regularizers removed.
Why does one model generalize well than the other?
What are the factors that help good generalization of the model?
