Lecture 2: Language Modelling, GPT, Decoding Strategies

Mitesh M. Khapra

AI4Bharat, Department of Computer Science and Engineering, IIT Madras

Introduction to Large Language Models

In the previous lecture, we learned about the components of the transformer architecture in the context of machine translation.

Multi-Head Attention

Feed forward NN

Add&Norm

Add&Norm

Multi-Head cross Attention

Feed forward NN

Add&Norm

Add&Norm

\sim
+
h_{source}
PE

Multi-Head Maksed Attention

Add&Norm

\sim
+
h_{target}
PE

In the previous lecture, we learned about the components of the transformer architecture in the context of machine translation.

Decoder

Encoder

At a high-level, we can just think of it as an encoder-decoder block

In the previous lecture, we learned about the components of the transformer architecture in the context of machine translation.

At an even higher level of abstraction, we can think of it as a black box that receives an input and produces an output.

Transformer

Text in source language

Translated text in target language

In the previous lecture, we learned about the components of the transformer architecture in the context of machine translation.

Transformer

Transformer

Transformer

Input text

Predict the class/sentiment

Input text

Summarize

Question

Answer

Input text

What if we want to use the transformer architecture for other NLP tasks?

We need to train a separate model for each task using dataset specific to the task

Transformer

Transformer

Transformer

Input text

Predict the class/sentiment

Input text

Summarize

Question

Answer

Input text

If we train the architecture from scratch (that is, by randomly initializing the parameters) for each task, it takes a long time for convergence

Often, we may not have enough labelled samples for many NLP  tasks

In the previous lectures, we learned  the components of transformer architecture in the context of machine translation.

What if we want to use the transformer architecture for other NLP tasks?

We need to train a separate model for each task using dataset specific to the task

Moreover, preparing labelled data is laborious and costly

On the other hand,

We have a large amount of unlabelled text easily available on the internet 

Transformer

Transformer

Transformer

Input text

Predict the class/sentiment

Input text

Summarize

Question

Answer

Input text

Can we make use of such unlabelled data to train a model?

Moreover, preparing labelled data is laborious and costly

On the other hand,

We have a huge unlabelled text data on the internet 

Can we make use of these unlabelled data to train a model?

Would that be helpful in adapting the model to downstream tasks with minimal fine-tuning (with zero or a few samples)? 

What will be the training objective in that case?

Transformer

Transformer

Transformer

Input text

Predict the class/sentiment

Input text

Summarize

Question

Answer

Input text

\times
\times
\times
\times
\times
\times

Module 2.1 : Language Modelling

Mitesh M. Khapra

AI4Bharat, Department of Computer Science and Engineering, IIT Madras

Motivation

" Wow, India has now reached the moon"

Is this sentence expressing a positive or a negative sentiment?

An excerpt from business today "What sets this mission apart is the pivotal role of artificial intelligence (AI) in guiding the spacecraft during its critical descent to the moon's surface."

Did the lander use AI for soft landing on the moon?

Assume that we ask questions to a lay person based on a statement or some excerpt

He likes to stay

He likes to stray

He likes to sway

Are these meaningful sentences?

The person will most likely answer all the questions, even though he/she may not be explicitly trained on any of these tasks. How?

We develop a strong understanding of  language through various language based interactions( listening/reading)  over our life time without any explicit supervision

Can a model develop basic understanding of language by getting exposure to a large amount of raw text? [pre-training]

More importantly, after getting exposed to such raw data can it learn to perform well on downstream tasks with minimum supervision? [Supervised Fine-tuning]

Idea

With this representation a linear model classifies reviews with 91.8% accuracy beating the SOTA (Ref)

...matches the performance of previous supervised systems using 30-100x fewer labeled examples (Ref)

Language Modeling

(Pre-training)

Raw text

Downstream tasks

(Fine-tuning)

(Samples and labels)

Language modelling

 Let \(\mathcal{V}\) be a vocabulary of  language (i.e., collection of all unique words in the language)

For example, if \(\mathcal{V}=\{an, apple, ate, I\}\), some possible sentences (not necessarily grammatically correct) are

Intuitively, some of these sentences are more probable than others.

We can think of a sentence as a sequence  \(X_1,X_2, \cdots,X_n\), where \(X_i \in \mathcal{V}\)

a. An apple ate I

b. I ate an apple 

c. I ate apple 

d. an apple 

e. .... 

What do we mean by that?

Intuitively, we mean that give a very very large corpus, we expect some of these sentences to appear more frequently than others (hence, more probable)

We are now looking for a function which takes a sequence as input and assigns a probability to each sequence

f:(X_1,X_2,\cdots X_n) \rightarrow [0,1]

Such a function is called a language model.

Language modelling

Definition

If we naively assume that  the words in a sequence are independent of each other then 

P(x_1,x_2,\cdots,x_T)=\prod \limits_{i=1}^T P(x_i)
P(x_1,x_2,\cdots,x_T)=
P(x_1)P(x_2|x_1)P(x_3|x_2,x_1) \cdots P(x_T|x_{T-1},\cdots,x_1)
=\prod \limits_{i=1}^T P(x_i|x_1,\cdots,x_{i-1})

How do we enable a model to understand language?

Simple Idea: Teach it the task of predicting the next token in a sequence..

You have tons of sequences available on the web which you can use as training data 

Roughly speaking, this task of predicting the next token in a sequence is called language modelling

?

However, we know that the words in a sentence are not independent but depend on the previous words

a. I enjoyed reading a book

b. I enjoyed reading a thermometer

The presence of "enjoyed" makes the word "book" more likely than "thermometer"

Hence, the naive assumption does not make sense

Current word \(\underbrace{x_i} \) depends on  previous words \(\underbrace{x_1,\cdots,x_{i-1}} \)

\prod \limits_{i=1}^T P(x_i|x_1,\cdots,x_{i-1}):

Current word \(\underbrace{x_i} \) depends on  previous words \(\underbrace{x_1,\cdots,x_{i-1}} \)

\prod \limits_{i=1}^T P(x_i|x_1,\cdots,x_{i-1}):

How do we estimate these conditional probabilities?

One solution: use autoregressive models where the conditional probabilities are given by parameterized functions with a fixed number of parameters (like transformers).

Causal Language Modelling (CLM)

P(x_1,x_2,\cdots,x_T)=
=P(x_1)P(x_2|x_1)P(x_3|x_2,x_1) \cdots P(x_T|x_{T-1},\cdots,x_1)
\prod \limits_{i=1}^T P(x_i|x_1,\cdots,x_{i-1})

We are looking for \(f_{\theta}\) such that

P(x_i|x_1,\cdots,x_{i-1})=f_\theta(x_i|x_1,\cdots,x_{i-1})

Can  \(f_{\theta}\) be a transformer?

Transformer

\(x_1,x_2,\cdots,x_{i-1}\)

\(P(x_i)\)

f_{\theta}

Using only the encoder of the transformer (encoder only models)

Using only the decoder of the transformer (decoder only models)

Using both the encoder and decoder of the transformer (encoder decoder models)

Multi-Head Attention

Feed forward NN

Add&Norm

Add&Norm

\(x_1,<mask>,\cdots,x_{T}\)

\(P(<mask>)\)

Multi-Head masked Attention

Feed forward NN

Add&Norm

Add&Norm

\(x_1,x_2,\cdots,x_{i-1}\)

\(P(x_i)\)

Multi-Head Attention

Feed forward NN

Add&Norm

Add&Norm

Multi-Head cross Attention

Feed forward NN

Add&Norm

Add&Norm

Multi-Head Maksed Attention

Add&Norm

\(x_1,<mask>,\cdots,x_{T}\)

\(<go>\)

\(P(<mask>)\)

Some Possibilities

Feed Forward Network

Masked Multi-Head (Self)Attention

Multi-Head (Cross) Attention

e
\langle \ go \rangle
x_1
x_2
x_3

The input is a sequence of words

We want the model to see only the present and past inputs.

We can achieve this by applying the mask.

M=\begin{bmatrix} 0&-\infty&-\infty & -\infty \\ 0&0&-\infty&-\infty\\ 0&0&0&-\infty\\ 0&0&0&0 \end{bmatrix}

The masked multi-head attention layer is required.

However, we do not need multi-head cross attention layer (as there is no encoder). 

Feed Forward Network

Masked Multi-Head (Self)Attention

p(x_1)
p(x_4|x_3,x_2,x_1)

The outputs represent each term in the chain rule

\cdots
=P(x_1)P(x_2|x_1)P(x_3|x_2,x_1) P(x_4|x_3,x_2,x_1)

However, this time the probabilities are determined by the parameters of the model,

=P(x_1;\theta)P(x_2|x_1;\theta)P(x_3|x_2,x_1;\theta) P(x_4|x_3,x_2,x_1;\theta)

Therefore, the objective is to maximize the likelihood \(L(\theta)\)

\langle go\rangle
x_1
x_2
x_3

Module 2.2 : Generative Pretrained Transformer (GPT)

Mitesh M. Khapra

AI4Bharat, Department of Computer Science and Engineering, IIT Madras

Generative Pretrained Transformer (GPT)

Now we can create a stack \((n)\) of modified decoder layers (called transformer block in the paper)

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 4

Transformer Block 5

p(x_1)
p(x_4|x_3,x_2,x_1)
\cdots
h_{l}=transformer\_block(h_{l-1}), \forall l \in [1,n]
h_{0}=X \in \mathbb{R}^{T \times d_{model}}

Let, \(X\) denote the input sequence 

h_1
h_2
h_3
h_4
h_5
P(x_i)=softmax(h_n[i]W_v)

Where \(h_n[i]\) is the \(i-\)the output vector in \(h_n\) block.

\mathscr{L}=\sum \limits_{i=1}^T \log (P(x_i|x_1,\cdots,x_{i-1}))
\langle \ go \rangle
x_1
x_2
x_3
W_v
W_v
h_{11}
h_{12}
h_{13}
h_{14}
h_{21}
h_{22}
h_{23}
h_{24}
h_{31}
h_{32}
h_{33}
h_{34}
h_{41}
h_{42}
h_{43}
h_{44}
h_{51}
h_{52}
h_{53}
h_{54}

Input data

BookCorpus

The corpus contains 7000 unique books, 74 Million sentences and approximately 1 Billion words across 16 genres

Also, uses long-range contiguous text

(i.e., no shuffling of sentences or paragraphs)

Side Note: The other benchmark dataset called 1B words could also be used. However, the sentences are not contiguous (no entailment)

Vocab size \(|\mathcal{V}|\): 40478

Tokenizer: Byte Pair Encoding

Embedding dim: \(768 \)

MODEL

Contains 12 decoder layers (transformer blocks)

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

p(x_1)
p(x_4|x_3,x_2,x_1)
\cdots
h_1
h_2
h_3
h_{12}
W_v
W_v
\vdots
\vdots
\vdots
\vdots

FFN hidden layer size: \(768 \times 4 = 3072\)

Attention heads: \(12 \)

Context size: \(512 \)

Dropout, layer normalization, and residual connections were implemented to enhance convergence during training.

Activation: Gaussian Error Linear Unit (GELU)

x_1
x_2
x_3
\langle \ go \rangle

Transformer Block 1

<go>

at

the

bell

labs

hamming

bound

...................

new

a

devising

..............

x_2
x_{18}
x_{351}
x_{511}

<stop>

A sample  data

Transformer Block 1

<go>

at

the

bell

labs

hamming

bound

...................

new

a

devising

..............

<stop>

Feed Forward Neural Network

Multi-head masked attention

<go>

at

the

bell

labs

hamming

bound

...................

new

a

devising

..............

<stop>

Masked Multi-head attention

Q
K
V
\text{MatMul:} \ Q^TK+M
\text{Scale}:\frac{1}{\sqrt{d_k}}
\text{Softmax}
\text{MatMul}
\text{dropout}
Q
K
V
\text{MatMul:} \ Q^TK+M
\text{Scale}:\frac{1}{\sqrt{d_k}}
\text{Softmax}
\text{MatMul}
\text{dropout}

Concatenate

Linear

Layer norm

Residual connection

\text{dropout}

<go>

at

the

bell

labs

hamming

bound

...................

new

a

devising

..............

<stop>

Masked Multi-head attention

Feed Forward Neural Network

z_1=\mathbb{R}^{768}
l={3042}
o_1=\mathbb{R}^{768}
\text{dropout}

Layer norm

Residual connection

Number of parameters

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

p(x_1)
p(x_4|x_3,x_2,x_1)
\cdots
h_1
h_2
h_3
h_{12}
W_v
W_v
\vdots
\vdots
\vdots
\vdots

token Embeddings: \(|\mathcal{V}| \times \) embedding_dim

40478 \times 768
=31 \times 10^6
=31M

Position Embeddings : context length \(\times\) embedding_dim

Embedding Matrix

512 \times 768
=0.3 \times 10^6
=0.3M

Total: \(31.3 M\)

The positional embeddings are also learned, unlike the original transformer which uses fixed sinusoidal embeddings to encode the positions.

x_1
x_2
x_3
\langle \ go \rangle

Number of parameters

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

p(x_1)
p(x_4|x_3,x_2,x_1)
\cdots
h_1
h_2
h_3
h_{12}
W_v
W_v
\vdots
\vdots
\vdots
\vdots

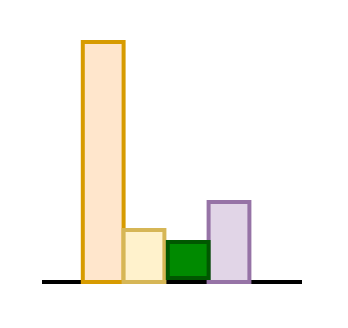
Attention parameters per block

W_Q=W_K=W_v=(768\times 64)

Per attention head

3 \times (768\times 64) \approx 147 \times 10^3

For 12 heads

12 \times 147 \times 10^3 \approx 1.7M

For a Linear layer:

768 \times 768 \approx 0.6M

For all 12 blocks

12 \times 2.3 = 27.6M
x_1
x_2
x_3
\langle \ go \rangle

Number of parameters

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

p(x_1)
p(x_4|x_3,x_2,x_1)
\cdots
h_1
h_2
h_3
h_{12}
W_v
W_v
\vdots
\vdots
\vdots
\vdots

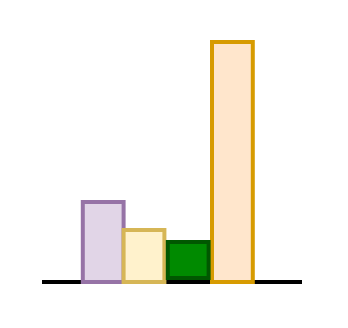
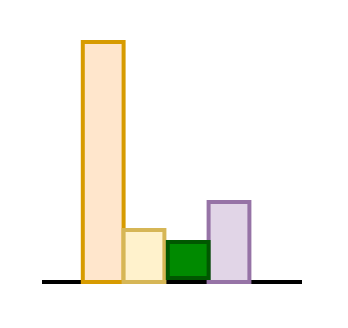
FFN parameters per block

2 \times(768 \times 3072)+3072+768 \\= 4.7 \times 10^{6}=4.7 M

For all 12 blocks

12 \times 4.7= 56.4 M
x_1
x_2
x_3
\langle \ go \rangle

Number of parameters

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

p(x_1)
p(x_4|x_3,x_2,x_1)
\cdots
h_1
h_2
h_3
h_{12}
W_v
W_v
\vdots
\vdots
\vdots
\vdots
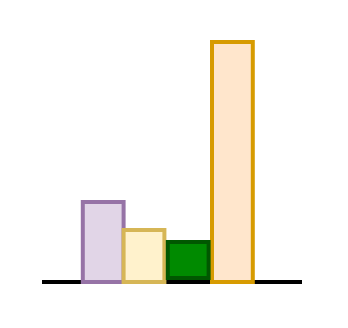
Layer Parameters (in Millions)
Embedding Layer
Attention layers
FFN Layers
Total

Embedding Matrix

31.3
27.6
56.4
116.461056^*

*Without rounding the number of parameters in each layer

Thus, GPT-1 has around 117 million parameters. 

x_1
x_2
x_3
\langle \ go \rangle

Module 2.3 : Pre-training and Fine Tuning

Mitesh M. Khapra

AI4Bharat, Department of Computer Science and Engineering, IIT Madras

Pre-Training

\mathscr{L}=-\sum \limits_{\mathbb{x}\in V:X \in \mathcal{X}} \sum \limits_{i=1}^T y_i\log (\hat{y_i}))

Minimize

Optimizer: Adam with cosine learning rate scheduler

Batch Size: 64

Input size: \((B,T,C)=(64,512,768)\), where, \(C\) is an embedding dimension 

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

\hat{y_1}
\hat{y_4}
\cdots
h_1
h_2
h_3
h_{12}
W_v
W_v
\vdots
\vdots
\vdots
\vdots

Embedding Matrix

Strategy : Teacher forcing (instead of auto-regressive training) for quicker and stable convergence

x_1
x_2
x_3
\langle \ go \rangle

Fine-tuning

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

\hat{y}
h_1
h_2
h_3
h_{12}
W_y
\vdots
\vdots
\vdots
\vdots

Embedding Matrix

x_1
x_2
\langle s \rangle
\langle e \rangle

Each sample in a labelled data set \(\mathcal{C}\) consists of a sequence of tokens \(x_1,x_2,\cdots,x_m\) with the label \(y\)

Initialize the parameters with the parameters learned by solving the pre-trianing objective

At the input side, add additional tokens based on the type of downstream task. For example, start  \(\langle s \rangle\) and end \(\langle e \rangle\) tokens for classification tasks

At the output side, replace the pre-training LM head with the classification head (a linear layer \(W_y\))

Fine-tuning involves adapting  model for various downstream tasks (with a minimal change in the architecture) 

Fine-tuning

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

\hat{y}
h_1
h_2
h_3
h_{12}
W_y
\vdots
\vdots
\vdots
\vdots

Embedding Matrix

Now our objective is to predict the label of the input sequence

\mathscr{L}=-\sum \limits_{(x,y)} \log (\hat{y_i})
\hat{y}=P(y|x_1,\cdots,x_m)
=softmax(W_yh_{l}^m)

Note that we take the output representation at the last time step of the last layer \(h_l^m\).

It makes sense as the entire sentence is encoded only at the last time step due to causal masking.

Then we can minimize the following objective 

Note that \(W_y\) is randomly initialized. Padding or truncation is applied if the length of input sequence is less or greater than the context length

h_{_{12}}^m
x_1
x_2
\langle s \rangle
\langle e \rangle

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

\hat{y}
h_1
h_2
h_3
h_{12}
W_y
\vdots
\vdots
\vdots
\vdots

Embedding Matrix

x_1
x_{2}
x_5
\langle s \rangle
\langle e \rangle

Sentiment Analysis

Text: Wow, India has now reached the moon

Sentiment: Positive

x_3
\hat{y} \in \{+1,-1\}
x_4

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

\hat{y}
h_1
h_2
h_3
h_{12}
W_y
\vdots
\vdots
\vdots
\vdots

Embedding Matrix

x_1
x_{k-1}
x_m
\langle s \rangle
\langle e \rangle

Textual Entailement/Contradiction

Text:  A soccer game with multiple males playing

Hypothesis:  Some men are playing a sport

Entailment: True

In this case, we need to use a delimiter token \(\langle \$ \rangle\) to differentiate the text from the hypothesis. 

\langle \$ \rangle
\cdots

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

h_1
h_2
h_3
h_{12}
\vdots
\vdots
\vdots
\vdots

Embedding Matrix

\langle s \rangle
\langle e \rangle

Multiple Choice

Question:  Which of the following animals is an amphibian?

Choice:  Frog

\langle \$ \rangle

Choice:  Fish

\(\leftarrow\) Question \(\rightarrow\)

\(\leftarrow\) Choice-1 \(\rightarrow\)

Feed in the question along with the choice-1

Linear-1

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

h_1
h_2
h_3
h_{12}
\vdots
\vdots
\vdots
\vdots

Embedding Matrix

\langle s \rangle
\langle e \rangle

Multiple Choice

Question:  Which of the following animals is an amphibian?

Choice:  Frog

\langle \$ \rangle

Choice:  Fish

\(\leftarrow\) Question \(\rightarrow\)

\(\leftarrow\) Choice-2 \(\rightarrow\)

Feed in the question along with the choice-2

Linear-2

Repeat this for all choices

Normalize via softmax

Linear-2

Linear-1

\hat{y}
W_y

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

h_1
h_2
h_3
h_{12}
\vdots
\vdots
\vdots
\vdots

Embedding Matrix

I
like
\langle s \rangle

Text Generation

Prompt:  I like

M=\begin{bmatrix} 0&0&0 & -\infty & -\infty \\ 0&0&0&-\infty & -\infty\\ 0&0&0&-\infty & -\infty\\ 0&0&0&0& -\infty \end{bmatrix}
W_v

Input:

Sequence length:  5

Output:

I like to think that

Feed in the prompt along with the mask and run the model in autregressive mode

Does it produce the same output sequence for the given prompt? 

or Will it be creative ?

Stoping Criteria:

or outputing a token: <e>

to

Wishlist for text generation

Discourage degenerative (that is, repeated or incoherent) texts

I like to think that I like to think...

I like to think that reference know how to think best selling book

Encourage it to be Creative in generating a sequence for the same prompt

I like to read a book

I like to buy a hot beverage 

I like a person who cares about others

Accelarate the generation of tokens 

Visualization Apps

https://huggingface.co/spaces/exbert-project/exbert

Something to ponder about

GPT and its versions are pre-trained on a large corpus, however, what if we want it to be domain specific? Like finanance

Pretrian the GPT on new text corpus specific to finance? or directly fine the GPT on supervised tasks related to finance

Language modeling can be useful outside of pre-training as well, for example to shift the model distribution to be domain-specific: using a language model trained over a very large corpus, and then fine-tuning it to a news dataset or on scientific papers e.g. LysandreJik/arxiv-nlp.

Module 2.4 : Decoding Strategies

Mitesh M. Khapra

AI4Bharat, Department of Computer Science and Engineering, IIT Madras

Decoding Strategies

Beam Search 

Top-P (Nucleus Sampling )

Greedy Search

Top-K sampling

Exhaustive Search

Deterministic

Stochastic

Contrastive Decoding

Decoding the most likely output sequence involves searching through all the possible output sequences based on their likelihood.

Therefore, the search problem is exponential in the length of the output sequence and is intractable (NP-complete) to search completely.

Exhaustive Search

|\mathcal{V}|^5

Exhaustively search for all possible sequences with the associated probabilities and output the sequence with the highest probability

I like cold water 

I like cold coffee

coffee like cold coffee

coffee coffee coffee coffee

I like I like

I like cold coffee

p(\cdot)=0.15

coffee like cold coffee

p(\cdot)=0.1

I like I like

p(\cdot)=0.001

I like coffee

p(\cdot)=0.12

coffee coffee coffee coffee

p(\cdot)=0.0001

I like cold water 

p(\cdot)=0.1

I like cold coffee

Outputs*

* Assuming the sequence has the highest probability among all \(|\mathcal{V}|^5\) sequences

Suppose that we want to generate a sequence of 5 words with the vocabulary \(\{ cold, coffee,I,like,water,<stop>\}\)

A
B
C
p(A|C)
p(B|C)
p(C|C)
p(A|B)
p(B|B)
p(C|B)
p(A|A)
p(B|A)
p(C|A)

t=1

t=2

max()
0.3
0.5
0.2
0.8
0.1
0.1
0.6
0.2
0.2
0.5
0.4
0.1
p(x_1,x_2)

Exhaustive search for a sequence of length 2 with the vocabulary of size 3

At time step-1, the decoder outputs probability for all 3  tokens

At time step-2, we need to run the decoder three times independently conditioned on all the three predictions from the previous time step

At time step-3 we will have to run the decoders 9 times

If \(|\mathcal{V}|=40000\), then we need to run the decoder 40000 times in parallel

Illustration

1 2 3 4 5

cold

<stop>

coffee

I

like

water

time steps

I

like

cold

coffee

<stop>

p(w_1=I)=0.4

At each time step, we always output the token with the highest probability (Greedy)

p(w_2=like|w_1=I)=0.35
p(w_3=cold|w_1,w_2)=0.45
p(w_4=coffee|w_1,w_2,w_3)=0.35
p(w_5=stop|w_1,w_2,w_3,w_4)=0.5
p(w_5,w_1,w_2,w_3,w_4)= \\ 0.5 \times 0.35 \times 0.45 \times0.35 \times0.4= 0.011

0.1

0.15

0.25

0.4

0.05

0.05

0.1

0.15

0.25

0.05

0.35

0.1

0.45

0.05

0.1

0.05

0.15

0.2

0.15

0.3

0.35

0.01

0.09

0.1

0.1

0.5

0.2

0.1

0.05

0.05

Then the probability of the generated sequence is

Greedy Search

On the other extreme we can do a greedy search 

1 2 3 4 5

cold

<stop>

coffee

I

like

water

time steps

I

like

cold

coffee

<stop>

p(w_5,w_1,w_2,w_3,w_4)= \\ 0.5 \times 0.35 \times 0.45 \times0.35 \times0.4= 0.011

0.1

0.15

0.25

0.4

0.05

0.05

0.1

0.15

0.25

0.05

0.35

0.1

0.45

0.05

0.1

0.05

0.15

0.2

0.15

0.3

0.35

0.01

0.09

0.1

0.1

0.5

0.2

0.1

0.05

0.05

Then the probability of the generated sequence is

Is this the most likely sequence?

What if we picked the second most probable token in the first time step?

What if we want to get a variety of sequences of the same length?

Some Limitations

If the starting token is the word "I", then it will always end up producing the same sequence:I like cold coffee

we would have ended up with a different sequence.

1 2 3 4 5

cold

<stop>

coffee

I

like

water

time steps

coffee

like

cold

water

<stop>

p(w_5,w_1,w_2,w_3,w_4)= \\ 0.5 \times 0.35 \times 0.45 \times0.35 \times0.4= 0.011

0.1

0.15

0.25

0.4

0.05

0.05

0.65

0.05

0.05

0.05

0.1

0.1

0.04

0.01

0.1

0.03

0.02

0.8

0.1

0.5

0.2

0.1

0.05

0.05

Then the probability of the generated sequence is

Then the conditional distribution in the subsequent time steps will change.

0.15

0.1

0.05

0.05

0.55

0.1

p(w_5,w_1,w_2,w_3,w_4)= \\ 0.25 \times 0.55 \times 0.65 \times0.8 \times0.5= 0.035

Then the probability of the generated sequence is

Why not follow this at every time step?

We could output this sequence instead of the one generated by greedy search.

Greedily selecting a token with max probability at every time step does not always give the sequence with maximum probability

What if we picked the second most probable token in the first time step?

Beam Search

Instead of considering probability for all the tokens at every time step (as in exhaustive search), consider only top\(-k\) tokens

t=1

0.5
0.4
0.1
0.1
0.2
0.5
0.2
0.2
0.6

t=2

A
B
C
p(A|A)
p(B|A)
p(C|A)
p(A|B)
p(B|B)
p(C|B)
\times
\times

Now we have to choose the tokens that maximize the probability of the sequence

\times
\times

 Suppose (\(k=2\))

p(A)p(A|A)=0.5 \times 0.1=0.05
p(A)p(B|A)=0.5 \times 0.2=0.01
p(A)p(C|A)=0.5 \times 0.5=0.25
p(B)p(A|B)=0.4 \times 0.2 =0.08
p(B)p(B|B) = 0.4 \times 0.2 =0.08
p(B)p(C|B) = 0.4 \times 0.6 =0.24

It requires \(k\times |\mathcal{V}|\) computations at each time step

Beam Search

Instead of considering probability for all the tokens at every time step (as in exhaustive search), consider only top\(-k\) tokens

t=1

0.5
0.4
0.1
0.1
0.2
0.5
0.2
0.2
0.6

t=2

0.55
0.25
0.2

t=3

A
B
C
p(A|A)
p(B|A)
p(C|A)
p(A|B)
p(B|B)
p(C|B)
0.1
0.75
0.15
p(B|C,A)
p(A|B,C)
P(A,C,B)=0.18
P(B,C,A)=0.13
0.25
0.24

 Suppose (\(k=2\))

Following the similar calculations, we end up choosing

Over

Beam Search

Instead of considering probability for all the tokens at every time step (as in exhaustive search), consider only top\(-k\) tokens

t=1

0.5
0.4
0.1
0.1
0.2
0.5
0.2
0.2
0.6

t=2

0.55
0.25
0.2

t=3

A
B
C
p(A|A)
p(B|A)
p(C|A)
p(A|B)
p(B|B)
p(C|B)

The parameter \(k\) is called beam size. It is an approximation to exhaustive search.

If \(k=1\), then it is equal to greedy search.

Now we will have \(k\)  sequences at the end of time step \(T\) and output the sequence which has the highest probability. 

0.1
0.75
0.15

It is a better approximation to exhaustive search.

p(B|C,A)
p(A|B,C)
P(A,C,B)=0.18
P(B,C,A)=0.13
A
train
steam
engine
track
engine
the
is
oil
train
turbine
is
spilled
making
made
a
the
costly
available
noise
sound
\langle stop \rangle
at

Now backtrack

A \ train \ engine \ is \ making \ the \ noise
A \ train \ engine \ oil \ is \ costly

Output the sequence which has the highest probability

Divide the probability of the sequence by its length (otherwise longer sequences will have lower probability)

Neither greedy search nor  beam search can result in creative outputs 

Both the greedy search and the beam search are prone to be degenerative

Latency for greedy search is lower than beam search

Note however that the beam search strategy is highly suitable for tasks like translation and summarization

We are surprised when something is creative!

Surprise = uncertaininty

Sampling Strategies

Top-K sampling

At every time step, consider \(top-k\) tokens from the probability distirbution

1 2 3 4 5

cold

<stop>

coffee

I

like

water

time steps

0.1

0.15

0.25

0.4

0.05

0.05

0.65

0.05

0.05

0.05

0.09

0.11

0.04

0.01

0.1

0.03

0.02

0.8

0.1

0.5

0.2

0.1

0.05

0.05

0.1

0.15

0.05

0.05

0.55

0.1

Sample a token from the top-k tokens!

Say, \(k=2\)

Let's generate a sequence using Top-K sampling

I

<stop>

I

<stop>

or it could have produced

The proability of top-k tokens will be normalized relatively,  \(P(I)=0.61,P(coffee)=0.39\) before sampling a token. 

Top-K sampling

1 2 3 4 5

cold

<stop>

coffee

I

like

water

time steps

0.1

0.15

0.25

0.4

0.05

0.05

0.65

0.05

0.05

0.05

0.09

0.11

0.04

0.01

0.1

0.03

0.02

0.8

0.1

0.5

0.2

0.1

0.05

0.05

0.1

0.15

0.05

0.05

0.55

0.1

coffee

like

cold

coffee

<stop>

coffee

like

cold

coffee

<stop>

How does random sampling help?

At every time step, consider \(top-k\) tokens from the probability distirbution

Sample a token from the top-k tokens!

Say, \(k=2\)

Let's generate a sequence using Top-K sampling

I

<stop>

or it could have produced

Surprise is an outcome of being random

How does beam search compare with human prediction at every time step?

Human predictions have a high variance whereas beam search predictions have a low variance.

Giving a chance to other highly probable tokens leads to a variety in the generated sequences.

Image source

What should the optimal value of k be?

she

said

,

"

I

never

thought

knew

had

saw

said

could

meant

\vdots

If we fix the value of,say, \(k=5\), then we are missing out other equally probable tokens from the flat distribution.

It will miss to generate a variety of sentences (less creative)

I

ate

the

pizza

while

it

was

still

hot

cooling

warm

on

heating

going

For a peaked distribution, using the same value of \(k=5\), we might end up creating some meaning less sentences

                   as we are taking tokens that are less likely to come next.

Solution-1:Low temparature sampling

P(x=u_l|x_{1:i-1})=\frac{exp(\frac{u_l}{T})}{\sum_{l'} exp(\frac{u_{l'}}{T})}

Given the logits, \(u_{1:|V|}\), and  temperature parameter \(T\), compute the probabilities as

Low temperature = skewed distribution = less creativity

high temperature = flatter distribution = more creativity

Solution:2 Top-P (Nucleus) sampling

Set a value for the parameter \(p, \ 0<p<1\).

Sum the probabilities of tokens starting from the top token.

Sort the probabilities in descending order 

If the sum exceeds \(p\), then sample a token from the selected tokens.

It is similar to \(top-k\) with \(k\) being dynamic. 

she

said

,

"

I

never

thought

knew

had

saw

said

could

meant

\vdots

I

ate

the

pizza

while

it

was

still

hot

cooling

warm

on

heating

going

Suppose we set \(p=0.6\),

For top left distribution: the model will sample from the tokens (thought,knew,had,saw,said)

For bottom left distribution: the model will sample from the tokens (hot,cooling)

Speculative Decoding/Assisted Generation

The various approaches that we have discussed so far was focusing on generating diverse and quality sentences but not on reducing the time complexity (or latency)

All tokens are generated sequentially in autoregressive sampling. Therefore, the time complexity to generate \(N\) tokens is \(O(N \cdot t_{model})\)

That's what the speculative decoding strategy try to address

It becomes a significant performance bottleneck for larger models.

Assigning 1 byte of memory requires 530GB of GPU memory

Assume a larger language model with 500+ Billion parameters.

This requires us to distribute the model across multiple GPUs (Model parallelism) that adds additional communication overhead to the final latency

To generate a single token, we need to carryout at least 500+ Billion operations

How? Let's see

(somehow) Parallelizing the process reduce the latency

Moreover, the sampling process is sequential

Rejection Sampling

Suppose we want to sample \(\tilde{x}\) from a complex distribution \(q(x)\) called target distribution.

Instead of directly sampling from the complex distribution \(q(x)\), we sample \(\tilde{x}\) from a simple distribution \(p(x)\) called draft distribution.

We accept or reject the sample \(\tilde{x}\) based on the following rule

\mathbb{I}=\frac{q(\tilde{x})}{c*p(\tilde{x})}>r

where \(\mathbb{I} \in \{0,1\}\) is an indicator variable and \(r \sim U(0,1)\) and \(c\) is a constant. The sample is accepted if \(\mathbb{I}=1\).

Note that a lot of samples got rejected! 

Out of 100 samples, only 15 were accepted. The efficiency is 0.15 percent!

Increasing efficiency requires us to assume reasonably better draft distribution!

Draft Model \(q(.|.)\)

7B parameters

We Apply the same idea here

Use a smaller but faster model (called draft model) that speculates (lookahead) \(K\) future(candidate) tokens in the Auto-Regressive manner

The more you learn
the
k=4
more
you  
can 
do

Draft Model \(p(.|.)\)

7B parameters

We Apply the same idea here

Use a smaller but faster model (called draft model) that speculates (lookahead) \(K\) future(candidate) tokens in the Auto-Regressive manner

k=5
p(x|x_1,\cdots,x_4)=argmax(p(.|.))=the

Using greedy search (for ex)

p(x|x_1,\cdots,x_4,x_5)=more
p(x|x_1,\cdots,x_4,x_5,x_6)=you
p(x|x_1,\cdots,x_4,x_5,x_6,x_7)=can
The more you learn
the
more
you  
can 
do
p(x|x_1,\cdots,x_4,x_5,x_6,x_7,x_8)=do

Target  \(q(.|.)\)

70 B parameters

Use a larget but slower model (called target model) that accepts or rejectis a subset of \(K\) tokens using some rejection criteria.

k=5+1
q(x=the|x_1,\cdots,x_4)

In Parallel, compute

q(x=more|x_1,\cdots,x_4,x_5)
q(x=you|x_1,\cdots,x_4,x_5,x_6)
q(x=can|x_1,\cdots,x_4,x_5,x_6,x_7)
The more you learn
q(the)
q(more)
q(you)  
q(can) 
q(do)
q(x=do|x_1,\cdots,x_4,x_5,x_6,x_7,x_8)
The more you learn the
The more you learn the more
The more you learn the more you can
The more you learn the more you can do
q(.)

Accept-Reject criterion

Now we have probabilities from both draft \(p(.|.)\) and target \(q(.|.)\)models. 

Remember that the propablities for the \(K\) tokens were computed in parallel by the target \(q(.|.)\)model. 

for \(t=1:K\):

           sample \(r \sim U(0,1)\)

           if \(r < min\big(1,\frac{q(x|x_1,\cdots,x_{n+t-1})}{p(x|x_1,\cdots,x_{n+t-1})}\big)\):

                     Accept the token: \(x_{n+t} \leftarrow x\) 

           else:

                     Resample from modified distribution

                     \(x_{n+t} \sim (q(x|x_1,\cdots,x_{n+t-1}) - p(x|x_1,\cdots,x_{n+t-1}))_+\)

                       exit for loop

If all tokens are accepted, sample \(K+1\)th token from \(q(.|.)\)

(f(x))_+= \frac{max(0,f(x))}{\sum_x max(0,f(x))}

What have we gained by Speculative Decoding?

At each iteration, it predicts atleast 1 (if all rejected) to atmost \(K+1\) tokens (if all accepted).

It reduces the time complexity from \(O(N \cdot t_{target}) \) to the best case of \(O(\frac{N}{K+1} \cdot (Kt_{draft}+t_{target}) \)

Contrastive Decoding

Expert Model

GPT-XL

Amateur Model

GPT-small

Barack Obama was born in Honolulu, Hawai. He was born in
0.27 Hawaii
0.18 the
0.16 Honolulu
0.10 1961
0.02 Washington
0.08 Honolulu
0.04 washington
0.04 the
0.001 1961
P_{exp}
P_{axp}

Prompt

 Greedy search

Barack Obama was born in Honolulu, Hawai. He was born in Hawai

 Top-k/Top-p

Barack Obama was born in Honolulu, Hawai. He was born in Washington

We are facing a problem of repetition and incoherence!

Consider only plausible tokens from the expert model using plausibility constraint.

Contrastive Decoding

Expert Model

GPT-XL

Amateur Model

GPT-small

Barack Obama was born in Honolulu, Hawai. He was born in
0.27 Hawaii
0.18 the
0.16 Honolulu
0.10 1961
0.02 Washington
0.08 Honolulu
0.04 washington
0.04 the
0.001 1961
log_{P_{exp}}-log_{P_{ama}}
P_{exp}
P_{axp}
4.6 1961
2.34 Hawaii
0.65 Honolulu
-0.73 Washington

Contrastive Decoding

Prompt

Barack Obama was born in Honolulu, Hawai. He was born in 1961

References

1. https://openai.com/research/language-unsupervised

2. Beam search strategies for Neural Machine Translation

3. The curious case of neural text degeneration

4. Decoding stratagies by Maxime Labonne

References

1. https://openai.com/research/language-unsupervised

2. Beam search strategies for Neural Machine Translation

3. The curious case of neural text degeneration

4. https://jaykmody.com/blog/speculative-sampling/

5. Speculative Sampling

6. Contrastive Decoding

Controlled text generation summary: https://lilianweng.github.io/posts/2021-01-02-controllable-text-generation/