imation
;is All you need
Arun Prakash A
Instructor
BS, IITM

Appro

\pi
import math
PI = math.pi=3.1415926
(Computer) Engineer
\pi
=3.14
Physicist


\pi
= \pi
Mathematician

Hilbert's name may
appear more often in the subsequent
talks!
No surprise!

Reasons for doing approximation

1.Storage and transmission
2.Computational efficiency
(In this talk)
Why do we care about storage in this modern era?

Most of the volume of internet data is occupied by
If data weights \(1 g\), then our earth would have turned into a black hole!

How I want you to see them..

f(t)
f(x,y)
f(x,y,t)
They are all functions!
Running example

f(t)
Let's start with a simple function
f(t)

f(t) = ?
f(t) = \sin(4 \times 10^3 \pi t)
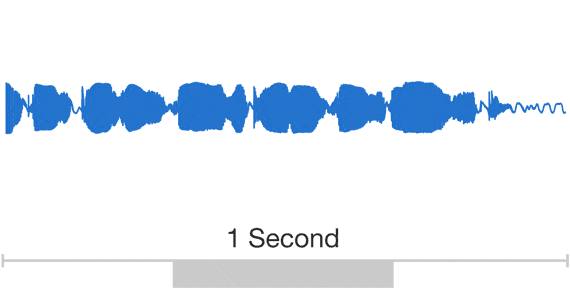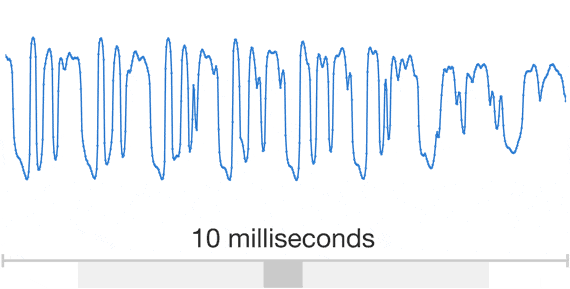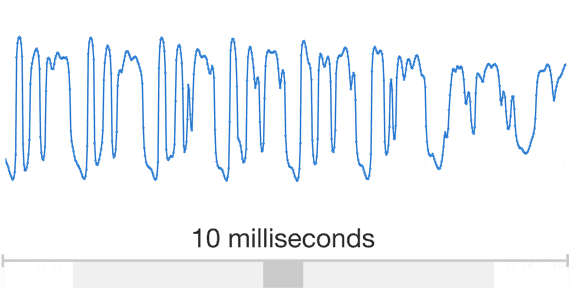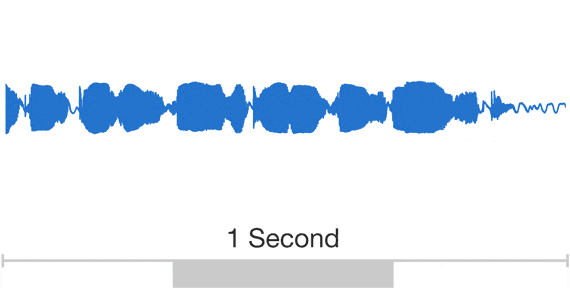
t (ms)
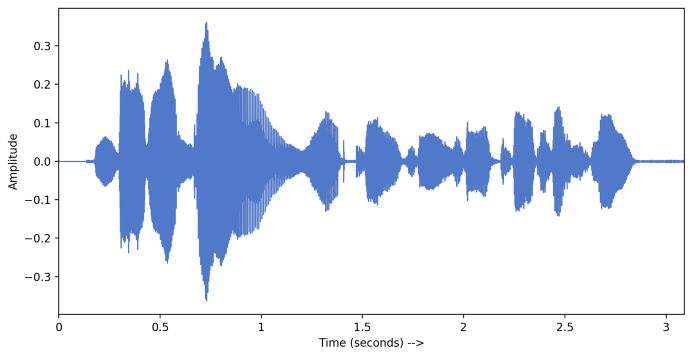
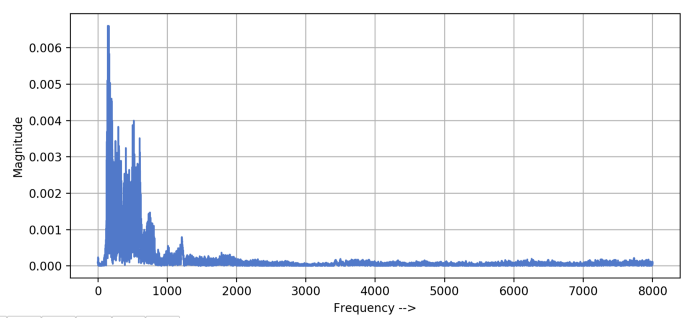
Let's hear it!

Well, the audio signals in the real world are continuous



How do we store it in a digital device?
Discretize/sampling
16000 samples/s
16 KB/s
56 MB for an hour of audio
280 hours of audio in 16GB Pendrive!

Wait a second,

\(k=4 \times 10^3\)
f(t) = \sin(4 \times 10^3 \pi t)


Generator: \(A sin(k\pi t)\)
( could be An algorithm inside a computer)
\(A,K\) needs to be stored, it takes
8 Bytes (32-bit processor)
Important Insight
If we have a well defined functional representation for the given waveform, we can store only their parameters such as \(A,k\) in the previous example

What about this function?
1
-1
T
f(t) = \begin{cases}
1 &\text{if } 0 < t <\frac{T}{2} \\
-1 &\text{if } \frac{T}{2} < t < T
\end{cases}
Constraints: (for some reasons)
- We can generate only sin waves
- As many as we wish
- Allowed to sum them up
Generator: \(A sin(k\pi t)\)
( could be An algorithm inside a computer)

Let's Approximate
f(t)
f(t)
= a_1\sin(k\pi t)
Is it a good approximation?
No
Memory : 8 B
k
a_1
Let's Approximate
f(t)
f(t)
=a_1\sin(k\pi t)

a_3\sin(3k\pi t)
Let's Approximate
f(t)
f(t)
=a_1\sin(k\pi t)+a_3\sin(3k\pi t)

a_3\sin(3k\pi t)
+
+
Do not bother about where is \(a_2\) and why not \(2k\) instead of \(3k\)
Let's Approximate
f(t)
f(t)
=a_1\sin(k\pi t)+a_3\sin(3k\pi t)
Is it a good approximation?
No, but better than previous..

Memory : 16 B
k
a_1
2k
2k
a_3
Author: Steve phelps
Let's see what happens if we "Sum" more terms
f(t)
=a_1\sin(k\pi t)+a_3\sin(3k\pi t)+a_5\sin(5k \pi t)+ \cdots+a_{49}\sin(11k\pi t)+ \cdots

Memory : 200 B
f(t) = \begin{cases}
1 &\text{if } 0 < t <\frac{T}{2} \\
-1 &\text{if } \frac{T}{2} < t < T
\end{cases}
Why not just store the definition of the function itself?
Well, good question!.
True, as long as We know what the form of function is
But the real world wave form is more complex than these simple functions

Any unwillingness to learn mathematics today can greatly restrict your possibilities tomorrow
Richard Hamming