Developing Deep Learning Models using

Arun Prakash A

IIT Madras

Core: tensors

JIT

Optim

multiprocessing

quantization

sparse

ONNX

Distributed

fast.ai

Detectron 2

Horovod

Flair

AllenNLP

torch.vision

BoTorch

GloW

Lightening

Skorch

import torch
import torch.nn as nn
import torch.nn.functional as F

class Model(nn.Module):
  
    def __init__(self, num_hidden):
        super(Model, self).__init__()
        self.layer1 = nn.Linear(28 * 28, 100)
        self.layer2 = nn.Linear(100, 50)
        self.layer3 = nn.Linear(50, 20)
        self.layer4 = nn.Linear(20, 1)
        self.num_hidden = num_hidden
    def forward(self, img):
        flattened = img.view(-1, 28 * 28)
        activation1 = F.relu(self.layer1(flattened))
        activation2 = F.relu(self.layer2(activation1))
        activation3 = F.relu(self.layer3(activation2))
        output = self.layer4(activation3)
        return output

The objective is not only

Build-Train-Test Deep Learning models

but also to Debug

Debugging requires a deeper understanding of things happening under the hood!

For the next two sessions, you most likely feel you are not doing deep learning

The Software Architecture of PyTorch

Tensor in

Tensor out

Operations on Tensors

Parameter Tensor in

Framework

What I build

Industry

Tech Giants

ATen

Cpp

JIT

Cpp

Autograd

Cpp

THC

Python

API

"A Tensor": ATen

"Caffe2 10": C10

Hardware Specific

torch

torch.autograd

torch.nn

torch. utils

CUDA,CPU,AMD,METAL

Tensor computation (like NumPy) with strong GPU acceleration

Deep neural networks built on a tape-based autograd system

Support efficient industry production at massive scale

Support exporting models to Python-less environment

Support for platforms of Caffe2 (iOS, Android, Raspbian, Tegra, etc) and will continue to expand various platforms support

torch.utils.data (now, TorchData)

TorchVision, TorchText modules

torch.tensor()

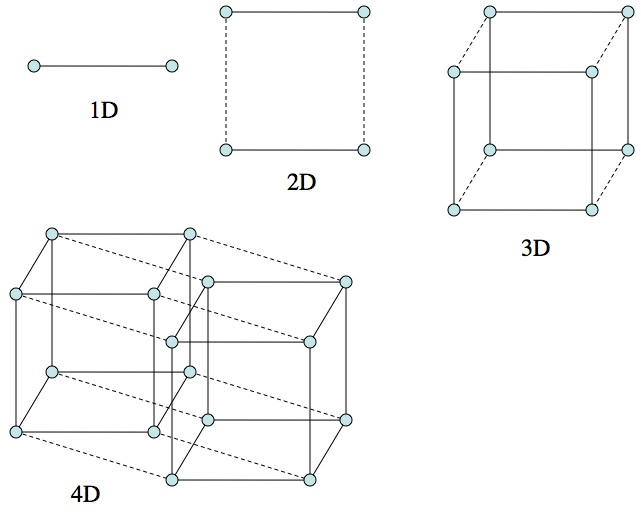
tensors

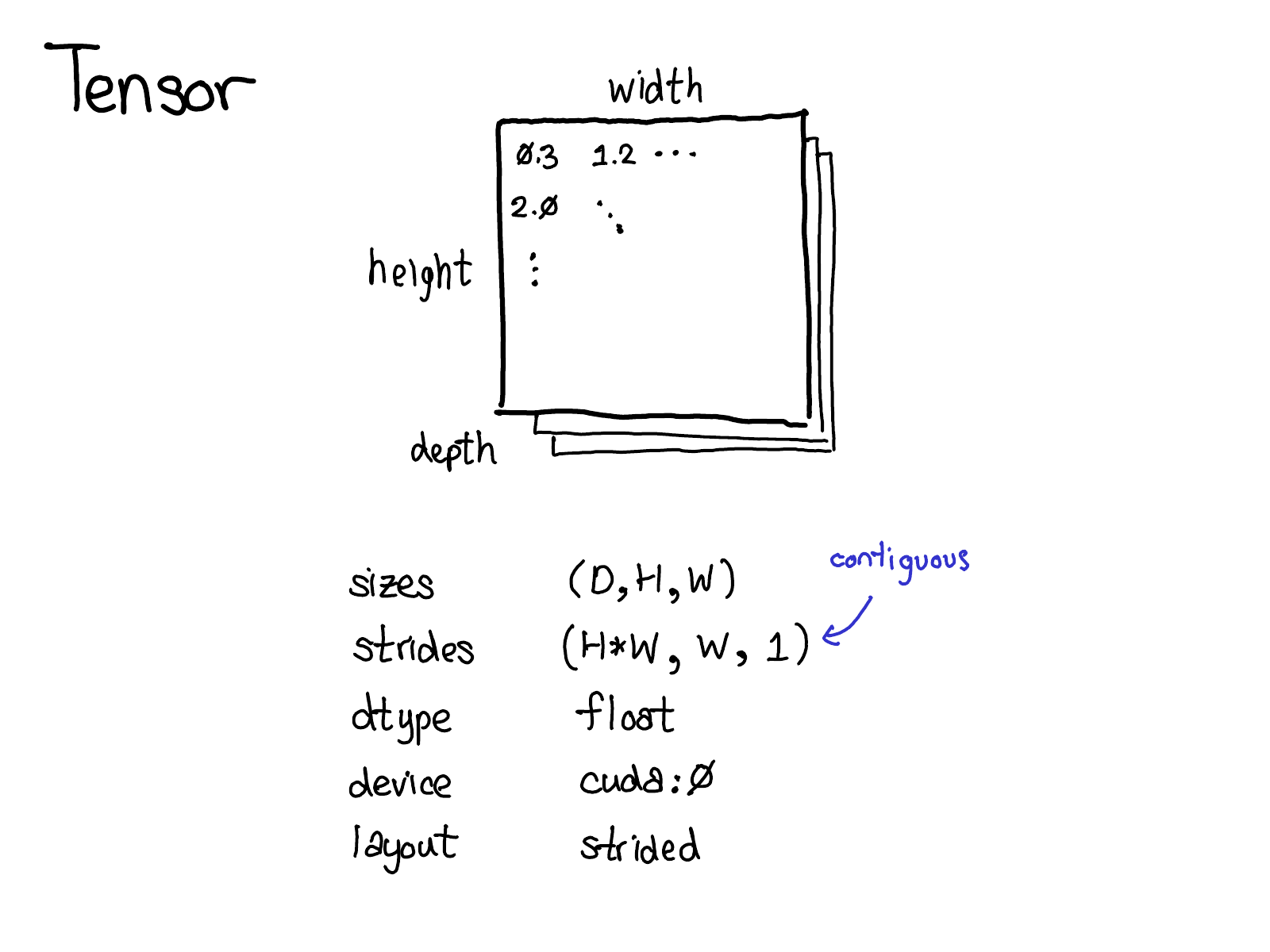
Concepts

Logical (view)

Physical

(Storage)

Stride

(Indexing)

Memory Layout

Devices

1	1.0	2	2.0

dtype

Limitations of using pure Python

List in python is in fact Linked List (Dynamic Array) under the hood

Python GIL (Global Interpreter Lock) which prevents Multiprocessing

This in turn affects the model training time (inevitably)

Source:http://blog.ezyang.com/2019/05/pytorch-internals/

Why should I Learn the internals?

Suppose we have a matrix of size \(X = 1000 \times 1000\)

Is transposing a costly operation?

How do you write a code to transpose? Looping?

Does accessing elements take constant time?

We can answer questions like these if we know how the tensors are actually stored in a hardware.

Is computing len(x) a costly operation?

Tensor
storage
stride
shape
device
size
grad
grad_fn
ndim

Tensor Object

\lbrace

Some useful/important attributes of a pytorch tensor

x = torch. Tensor([])

Tensor
storage
stride
shape
device
size
grad
grad_fn
ndim

Tensor Object

Usually, all tensors are created in CPU (unless, explicitly set to GPU).

We can move back and forth between CPU and GPU, however, it is a costlier operation for a large tensors!

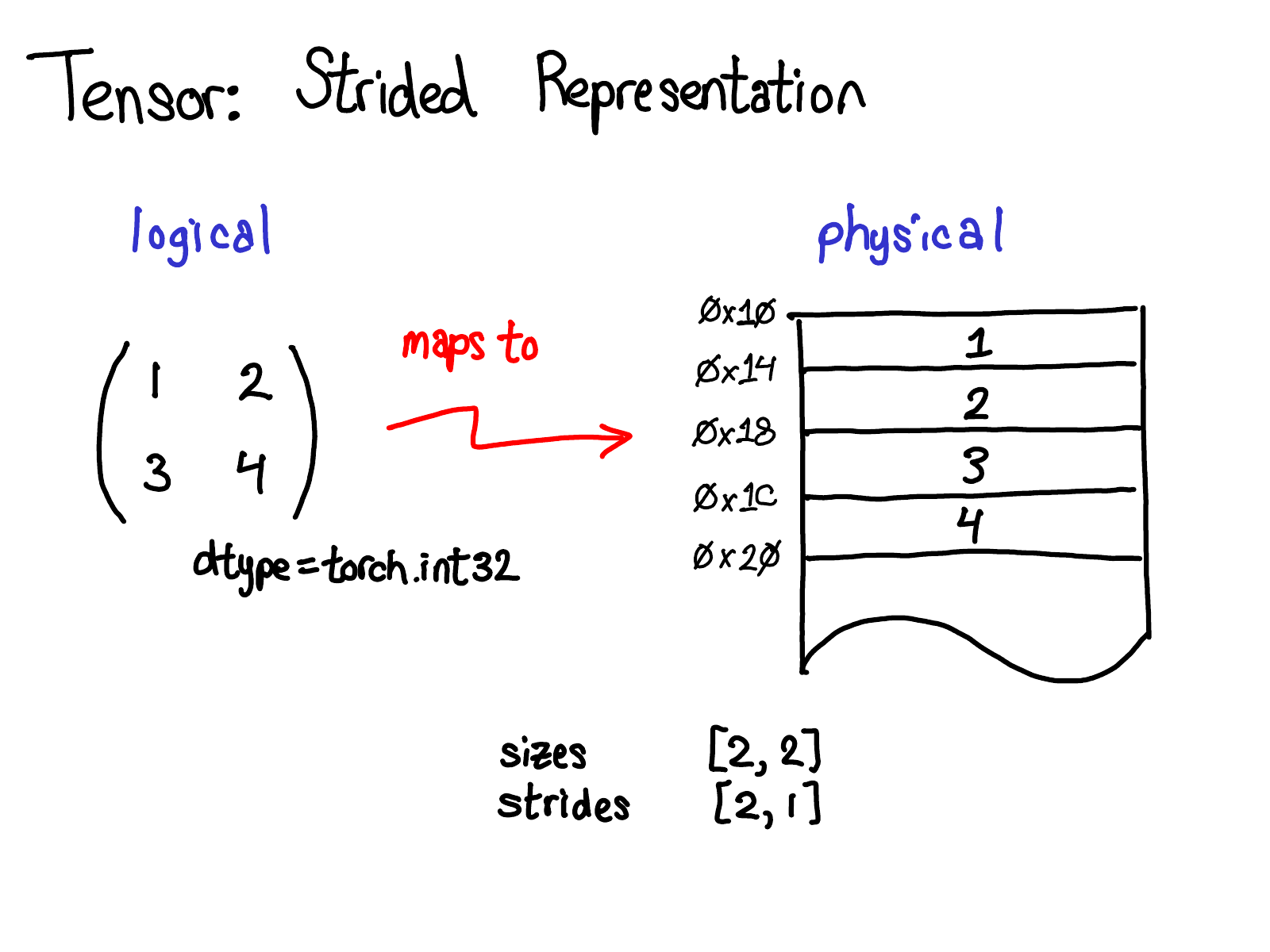
Maping follows a row-major form

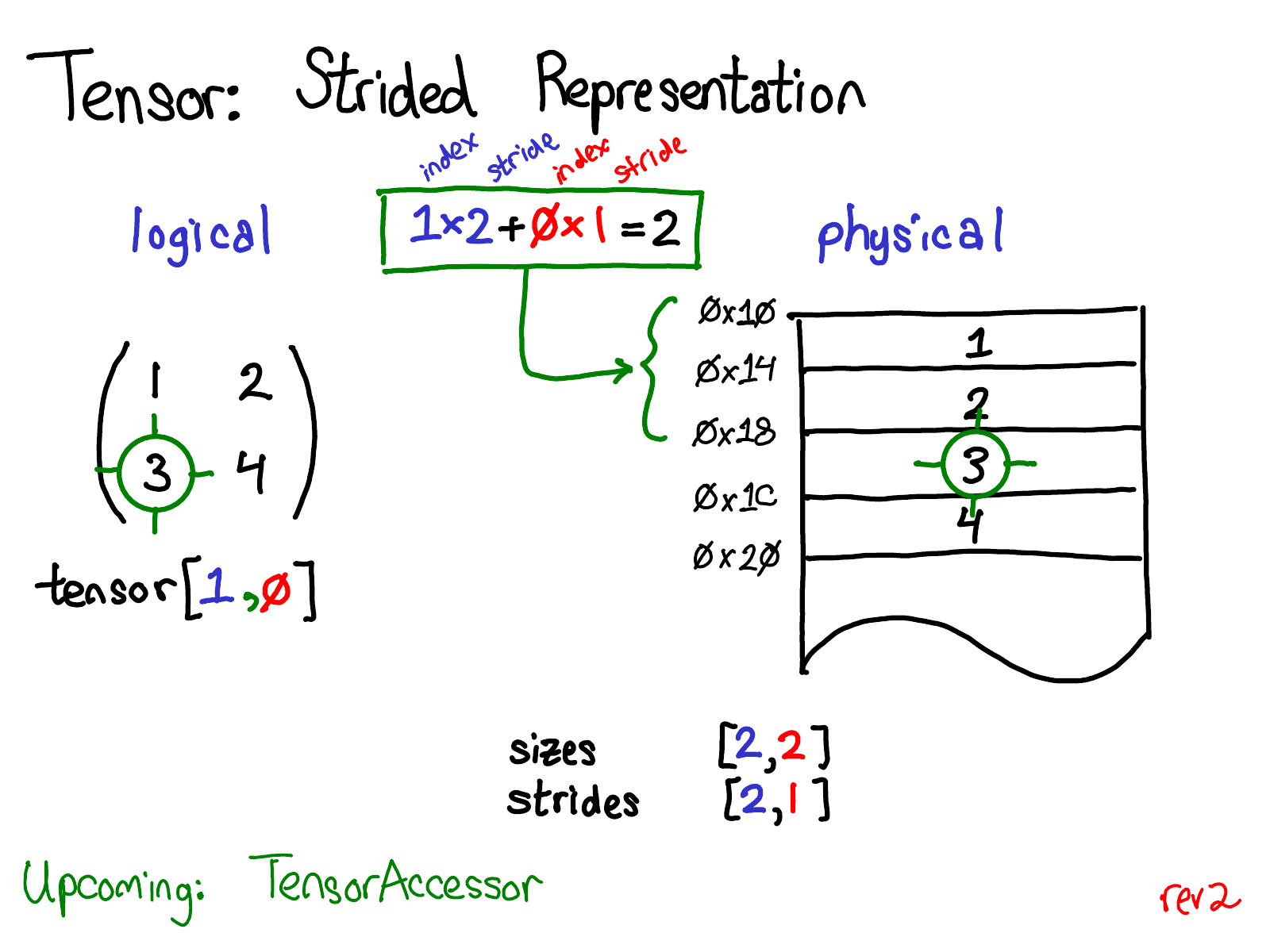
Source:http://blog.ezyang.com/2019/05/pytorch-internals/

The other representation is sparse representation

Source:http://blog.ezyang.com/2019/05/pytorch-internals/

Dispatching

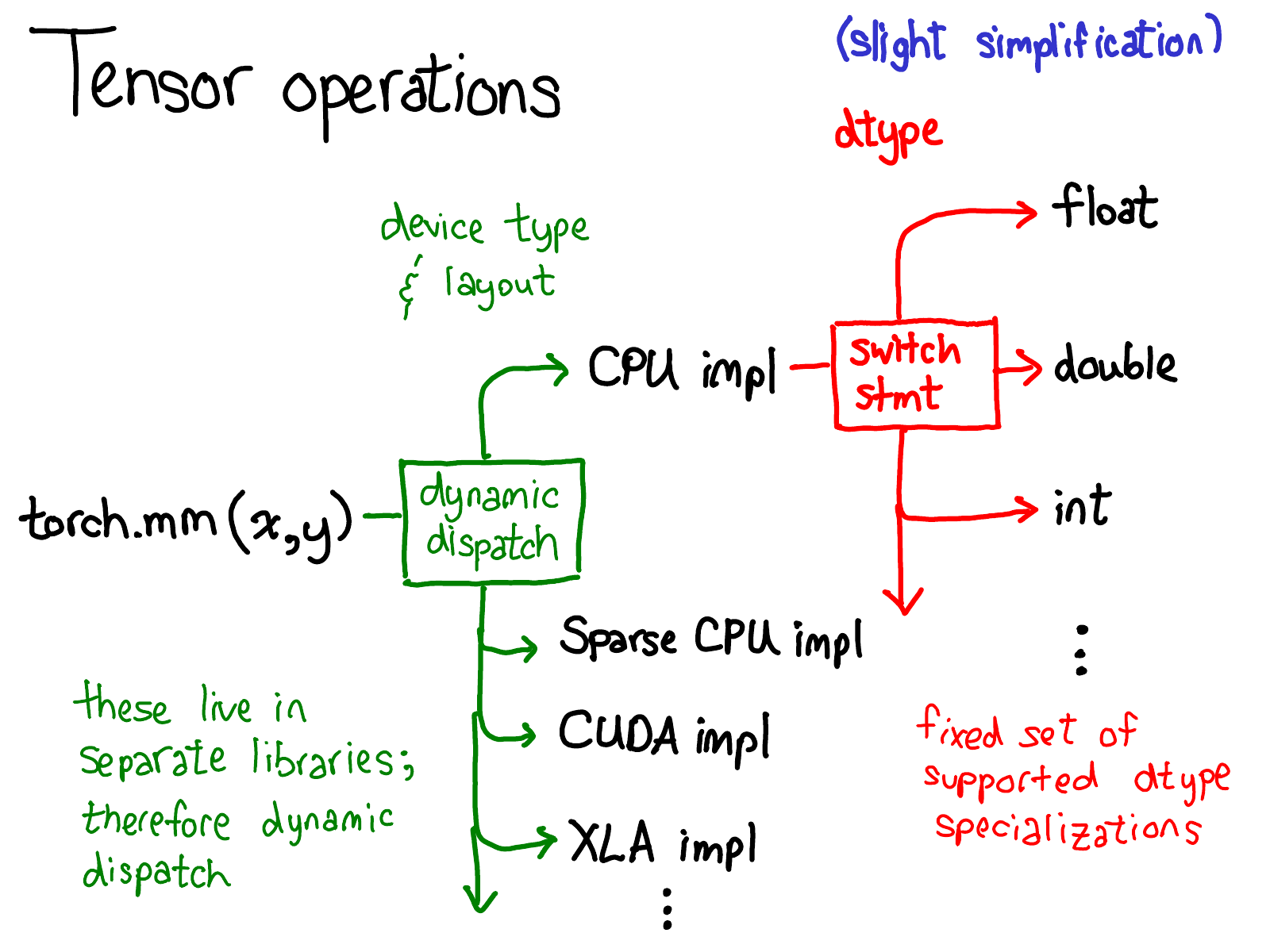
Source:http://blog.ezyang.com/2019/05/pytorch-internals/

Physical storage

Logical View

Source:istock

Dimensions/axis/coordinate

0.1

x = torch. Tensor(0.1)

x[0]

invalid index of a 0-dim tensor

x.item()

Dim: 0

Memory location

Dimensions/axis/coordinate

0.1	0.2	0.3

x = torch. Tensor([0.1,0.2,0.3])

x[0]
>>0.1

Dim: 1

Stride: 1

Contiguous memory

Dimensions/axis/coordinate

0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1

x = torch. Tensor([[0.1,0.2,0.3],[0.4,0.5,0.6],[0.7,0.8,0.9]])

x[1]

Dim: 2

stride: (3,1)

[d0*d0_stride + d1*d1_stride]

[1*3+
0*1 = 3]

It is alright to view this as a matrix but not always helpful when we deal with high dim tensors

Dimensions/axis/coordinate

0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1

x = torch. Tensor([[0.1,0.2,0.3],[0.4,0.5,0.6],[0.7,0.8,0.9]])

torch.sum(x,dim=0)

Dim: 2

stride: (3,1)

[d0*d0_stride + d1*d1_stride]

1.2

shape: (3,3)

Range:d0={0,1,2}

Range:d1={0,1,2}

since sum is across dim:0, vary dim:0 to its range (inner loop) and then dim:1 (outer loop)

0*3+ 0*1=0, x[0]=0.1

1*3+ 0*1=3, x[3]=0.4

2*3+ 0*1=6, x[6]=0.7

\sum

=1.2

Dimensions/axis/coordinate

0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1

x = torch. Tensor([[0.1,0.2,0.3],[0.4,0.5,0.6],[0.7,0.8,0.9]])

torch.sum(x,dim=0)

Dim: 2

stride: (3,1)

[d0*d0_stride + d1*d1_stride]

1.2	1.5

shape: (3,3)

Range:d0={0,1,2}

Range:d1={0,1,2}

since sum is across dim:0, vary dim:0 to its range (inner loop) and then dim:1 (outer loop)

0*3+ 1*1=1, x[1]=0.2

1*3+ 1*1=4, x[4]=0.5

2*3+ 1*1=7, x[7]=0.8

\sum

=1.5

Dimensions/axis/coordinate

0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1

x = torch. Tensor([[0.1,0.2,0.3],[0.4,0.5,0.6],[0.7,0.8,0.9]])

torch.sum(x,dim=0)

Dim: 2

stride: (3,1)

[d0*d0_stride + d1*d1_stride]

1.2	1.5	1.8

shape: (3,3)

Range:d0={0,1,2}

Range:d1={0,1,2}

since sum is across dim:0, vary dim:0 to its range (inner loop) and then dim:1 (outer loop)

0*3+ 2*1=2, x[1]=0.3

1*3+ 2*1=5, x[4]=0.6

2*3+ 2*1=8, x[7]=0.9

\sum

=1.8

Dimensions/axis/coordinate

0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1

x = torch. Tensor([[0.1,0.2,0.3],[0.4,0.5,0.6],[0.7,0.8,0.9]])

torch.sum(x,dim=1)

Dim: 2

stride: (3,1)

[d0*d0_stride + d1*d1_stride]

0.6

shape: (3,3)

Range:d0={0,1,2}

Range:d1={0,1,2}

since sum is across dim:1 now, vary dim:1 to its range (inner loop) and then dim:1 (outer loop)

0*3+ 0*1=0, x[0]=0.1

0*3+ 1*1=1, x[1]=0.2

0*3+ 2*1=2, x[2]=0.3

\sum

=0.6

Dimensions/axis/coordinate

0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1

x = torch. Tensor([[0.1,0.2,0.3],[0.4,0.5,0.6],[0.7,0.8,0.9]])

torch.sum(x,dim=1)

Dim: 2

stride: (3,1)

[d0*d0_stride + d1*d1_stride]

0.6	1.5

shape: (3,3)

Range:d0={0,1,2}

Range:d1={0,1,2}

since sum is across dim:1 now, vary dim:1 to its range (inner loop) and then dim:1 (outer loop)

1*3+ 0*1=3, x[3]=0.4

1*3+ 1*1=1, x[4]=0.5

1*3+ 2*1=2, x[5]=0.6

\sum

=1.5

Dimensions/axis/coordinate

0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8

x = torch.tensor([[[0.1,0.2],[0.3,0.4]],[[0.5,0.6],[0.7,0.8]]])

Dim: 3

torch.sum(x,dim=1)

Let's figure out the shape of the tensor by starting with the right most dimension

\(d_k=2 \) (because there are two numbers (scalars) enclosed by a square bracket

\(d_{k-1} =2 \) (because there are two vectors (dim:1) enclosed by a square bracket

\(d_{k-2} =1 \)

Dimensions/axis/coordinate

0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8

x = torch.tensor([[[0.1,0.2],[0.3,0.4]],[[0.5,0.6],[0.7,0.8]]])

Dim: 3

torch.sum(x,dim=1)

stride: (4,2,1)

[d0*d0_stride + d1*d1_stride+d2*d2_stride]

shape: (1,2,2)

Range:d0={0,1,2}

Range:d1={0,1,2}

x:2 \times 2 \times 3 \times 2

torch.sum(x,dim=2)

stride: (12,6,2,1)

Range:d0={0,1}

Range:d1={0,1}

Range:d2={0,1,2}

Range:d3={0,1}

d0*12	d1*6	d2*2	d3*1
0	0	0	0
		1
		2

index: 0+0+0+0=0, x[0]=0

index: 0+0+2+0=0, x[2]=1

index: 0+0+4+0=0, x[4]=0

\sum

x:2 \times 2 \times 3 \times 2

torch.sum(x,dim=2)

stride: (12,6,2,1)

Range:d0={0,1}

Range:d1={0,1}

Range:d2={0,1,2}

Range:d3={0,1}

d0*12	d1*6	d2*2	d3*1
0	0	0
		1	1
		2

index: 0+0+0+1=1, x[1]=2

index: 0+0+2+1=3, x[3]=1

index: 0+0+4+1=0, x[5]=2

\sum

Move into the right adjacent dimension

x:2 \times 2 \times 3 \times 2

torch.sum(x,dim=2)

stride: (12,6,2,1)

Range:d0={0,1}

Range:d1={0,1}

Range:d2={0,1,2}

Range:d3={0,1}

d0*12	d1*6	d2*2	d3*1
0		0	0
	1	1
		2

index: 0+6+0+0=6, x[6]=1

index: 0+6+2+0=8, x[8]=1

index: 0+6+4+0=10, x[10]=1

\sum

Move into left adjacent dimension

x:2 \times 2 \times 3 \times 2

2 \times 2 \times 3 \times 2

We call the 'sum' a reduction operation as it reduces the dim from 3 to 1.

2 \times 2 \times 2

2 \times 3 \times 2

torch.sum(x,dim=2)

torch.sum(x,dim=1)

2 \times 2 \times 3

torch.sum(x,dim=3)

3 \times 5 \times 5 \times 5

All these cubes are the elements at 0-th dim of a tensor of shape \(3 \times 5 \times 5 \times 5\). The first number 3 denotes three elements in zeroth dim and each of size 5 x 5 x 5 and

Let's switch to Colab Notebook

Cautions

1. Casting a Numpy array to a torch tensor ( vice-versa) shares a common memory (buffer). Changing one affects the other

2. Avoid in place operations (or be conscious of it) as it affects back prop and hence gives raise to unexpected results

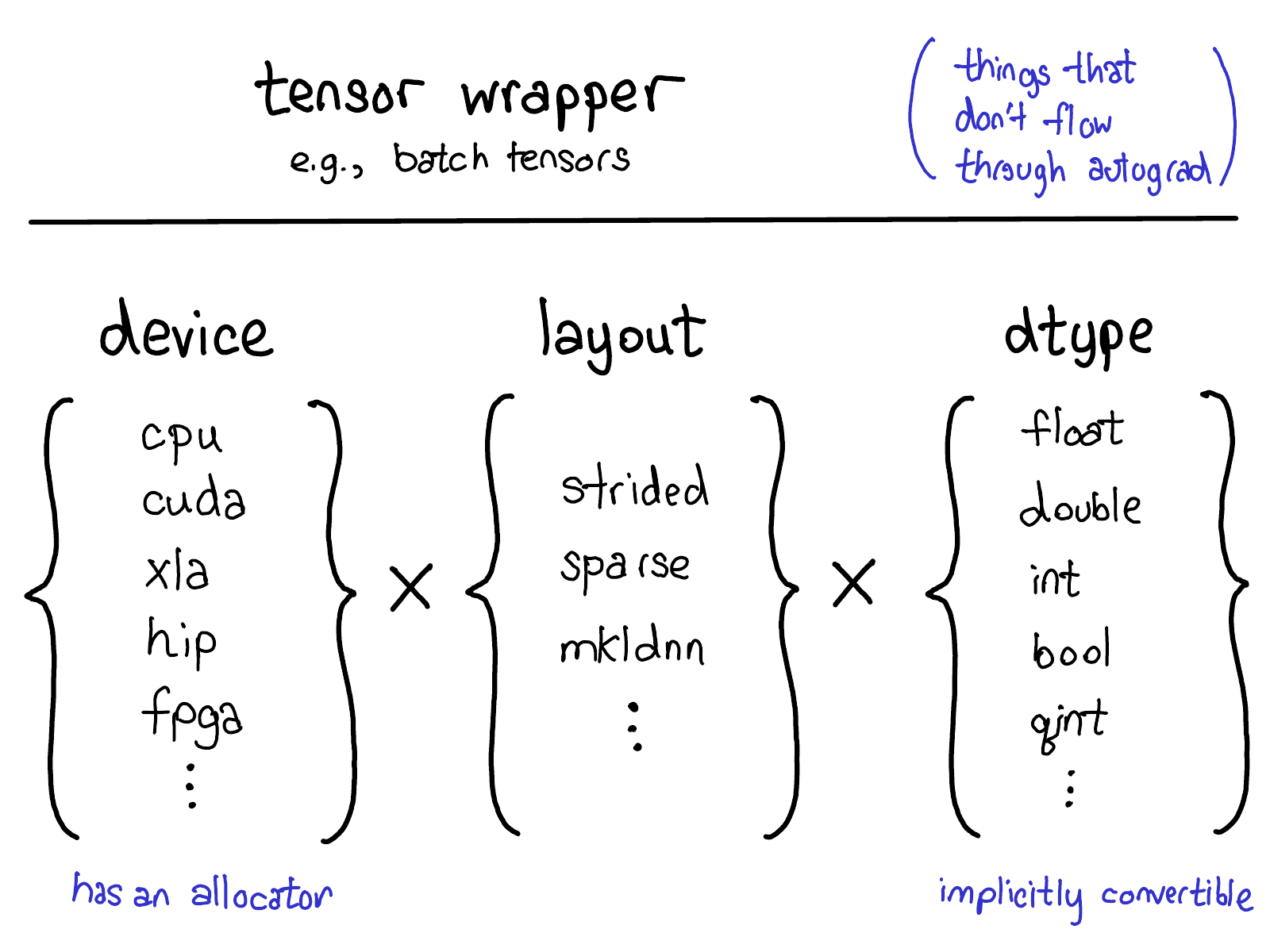
torch.autograd()

Developing Deep Learning Models using

Pytorch

Arun Prakash A

DL Course Instructor

BS, IIT Madras

Recap

Tensor in

Tensor out

Operations on Tensors

Parameter Tensor in

Focus of the session!

Tensor
storage
stride
shape
device
size
grad
grad_fn
req_grad
backward

Tensor Object

Objective

Understnad how gradients are computed for a given tensor using a computational graph

\nabla w=\sum \quad(\hat{y}-y) \quad \sigma(x)(1-\sigma(x))\quad x

.grad_fn

(lossBackward)

.grad_fn

ctx._savedTensor

Accumulate

.grad

Gradient computation for a single sigmoid neuron

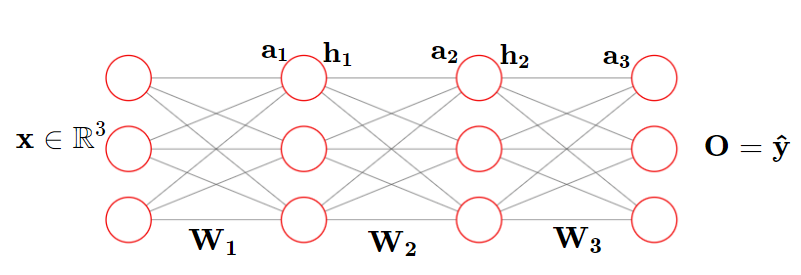
Requirements to compute backprop for any NN?

Forward Prop	Back-Prop

(10+) Activation functions

Gradient function for those activation functions

Matmul, \(Wx\)

Gradient function for Matmul, \(W^T\)

Conv, \(W * x\)

Gradient function for convolution

In general, we need gradient functions for all the operations used in the forward propagation

ConCat, \([x_1, x_2]\)

Gradient function for concatenation

AutoGrad is not FiniteDiff

AutoGrad is tape-based autodiff

Maintain a list of functions (operators) with the way to compute gradients for them

def sigmoid():
  
  def propagate():
    
    pass

def tanh():
  
  def propagate():
    
    pass

def add():
  
  def propagate():
    
    pass

def matmul():
  
  def propagate():
    
    pass

z = x * y

def mul(x,y):
  z = x*y

\frac{\partial z}{\partial x}=y

\frac{\partial z}{\partial y}=x

\frac{\partial L}{ \partial z}

\frac{\partial L}{\partial x}=\frac{\partial L}{\partial z} \frac{\partial z}{\partial x}

\frac{\partial L}{\partial y}=\frac{\partial L}{\partial z} \frac{\partial z}{\partial y}

def mul(x,y):
  '''
  The clousre:
     Outer scope variables are x,y,z.
     These are binded to the nested function propagate for backprop
  '''
  z = x*y
  def propagate(dLdz):
    dLdx = dLdz*y
    dLdy = dLdz*x
    return (dLdx,dLdy)
    # store it in a tape
    gradient_tape.append([x,y,propagate])
    
  return z

\frac{\partial L}{\partial x}=\frac{\partial L}{\partial z} y

\frac{\partial L}{\partial y}=\frac{\partial L}{\partial z} x

grad_fn = <MulBackward>

z = x + y

\frac{\partial z}{\partial x}

\frac{\partial z}{\partial y}

\frac{\partial L}{ \partial z}

\frac{\partial L}{\partial x}=\frac{\partial L}{\partial z} \frac{\partial z}{\partial x}

\frac{\partial L}{\partial y}=\frac{\partial L}{\partial z} \frac{\partial z}{\partial y}

def add(x,y):
  '''
  The clousre:
     Outer scope variables are x,y,z.
     These are binded to the nested function propagate for backprop
  '''
  z = x+y
  def propagate(dLdz):
    dLdx = dLdz
    dLdy = dLdz
    return (dLdx,dLdy)
    # store it in a tape
    gradient_tape.append([x,y,propagate])
    
  return z

\frac{\partial L}{\partial x}=\frac{\partial L}{\partial z}

\frac{\partial L}{\partial y}=\frac{\partial L}{\partial z}

grad_fn = <AddBackward>

z = Wx+b

\frac{\partial z}{\partial x}

\frac{\partial L}{ \partial z}

\frac{\partial L}{\partial x}=\frac{\partial L}{\partial z} \frac{\partial z}{\partial x}

def matmul(x,y):
  '''
  The clousre:
     Outer scope variables are x,y,z.
     These are binded to the nested function propagate for backprop
  '''
  z = x+y
  def propagate(dLdz):
    dLdx = dLdz
    dLdy = dLdz
    return (dLdx,dLdy)
    # store it in a tape
    gradient_tape.append([x,y,propagate])
    
  return z

\frac{\partial L}{\partial x}= W^T\frac{\partial L}{\partial z}

grad_fn = <AddmmBackward>

Assuming denominator layout

z = \sigma(x)

\frac{\partial z}{\partial x}

\frac{\partial L}{ \partial z}

\frac{\partial L}{\partial x}=\frac{\partial L}{\partial z} \frac{\partial z}{\partial x}

def tanh(x):
  '''
  The clousre:
     Outer scope variables are x,y,z.
     These are binded to the nested function propagate for backprop
  '''
  z = sigmoid(x)
  
  def propagate(dLdz):
    dLdx = dLdz*dtanh(x)
    
    return (dLdx)
    # store it in a tape
    gradient_tape.append([x,propagate])
    
  return z

\frac{\partial L}{\partial x}=\frac{\partial L}{\partial z} \sigma'(x)

\sigma()

grad_fn = <TanhBackward>

Pytorch already has implemented forward-backward calls for so many Functions (Operations)

Those includes matmul, activation, add, slice,concat,..Let's call these as elementary functions for convenience

What if I want to implement the same for a new Function(operation)? (of course, it is less likely unless you are doing a research in the core domain)

from torch.autograd import Function

class FFT(Function):  
     @staticmethod
     def forward(ctx, i,nfft):
        result = fft(i,nfft)
        ctx.save_for_backward(result)
        return result

     @staticmethod
     def backward(ctx, grad_output):
         result, = ctx.saved_tensors
        return grad_output * result

 # Use it by calling the apply method:
 output = FFT.apply(input)

from torch.autograd import Function

Use `Function` class from `autograd` module and define `forward` and `backward` methods for that function

In fact, the entire computational graph (will discuss next) is composed of `Function` objects

The following slides are inspired from https://www.youtube.com/watch?v=MswxJw-8PvE

data	(1,n)
grad	None
grad_fn	None
req_grad	bool
backward	method
is_leaf	bool

x=torch.tensor((1,n))

Those requirements are the attributes (args) of a tensor we create

data	1.0
grad	None
grad_fn	None
req_grad	True
backward	method
is_leaf	True

x=torch.tensor(1.0,requires_grad=True)

Because we created this tensor.The tensor is not a result of some operations

y=torch.sigmoid(x)

data
grad
grad_fn
req_grad
backward
is_leaf

Fill the attributes!

data	1.0
grad	None
grad_fn	None
req_grad	True
backward	method
is_leaf	True

x=torch.tensor(1.0,requires_grad=True)

y=torch.sigmoid(x)

data	0.73
grad	None
grad_fn	SigmoidBackward
req_grad	True
backward	method
is_leaf	False

y is now a result of some differentiable operation. So, no longer a leaf variable

x = torch.tensor(1.0,requires_grad=True)
y = torch.sigmoid(x)
z = 2*y

non-leaf node

grad_fn

pointer of a tensor attrib

data flow

leaf node

grad_fn

Let's see what happens during backprop..

\sigma(x)

SigmoidBackward

Mul

MulBackward

Forward Prop

x = torch.tensor(1.0,requires_grad=True)
y = torch.sigmoid(x)
z = 2*y

\sigma(x)

non-leaf node

SigmoidBackward

grad_fn

pointer of a tensor attrib

data flow

Mul

leaf node

grad_fn

MulBackward

\frac{\partial z}{\partial z}=1

Backprop

\frac{\partial z}{\partial x}=\frac{\partial z}{\partial y}\frac{\partial y}{\partial x}

x = torch.tensor(1.0,requires_grad=True)
y = torch.sigmoid(x)
z = 2*y

\sigma(x)

non-leaf node

SigmoidBackward

grad_fn

pointer of a tensor attrib

Mul

leaf node

grad_fn

MulBackward

\frac{\partial z}{\partial z}=1

Backprop

ctx._saved_tensor:
[_saved_other = 2,
_saved_self = None]

next_functions:

[ (SigmoidBackward),None)]

\frac{\partial z}{\partial y}=2

\frac{\partial z}{\partial x}=\frac{\partial z}{\partial y}\frac{\partial y}{\partial x}

.grad=\frac{\partial z}{\partial y}=2

data flow

x = torch.tensor(1.0,requires_grad=True)
y = torch.sigmoid(x)
z = 2*y

\sigma(x)

non-leaf node

SigmoidBackward

grad_fn

pointer of a tensor attrib

data flow

Mul

leaf node

grad_fn

MulBackward

\frac{\partial z}{\partial z}=1

Backprop

\frac{\partial z}{\partial y}=2

\frac{\partial y}{\partial x}=(1-\sigma(x)) \sigma(x)\\ \quad \quad =0.73*0.27=0.1971

\frac{\partial z}{\partial x}=\frac{\partial z}{\partial y}\frac{\partial y}{\partial x}

.grad=\frac{\partial z}{\partial y}=2

ctx._saved_tensor:
[_saved_result = 0.73]

next_functions:

[ (AccumulateGrad)]

x.grad=\frac{\partial z}{\partial x}=0.39

AccumulateGrad

Why do we need such a complicated way?

Generalization,
Differentiable Programming

Let's switch to colab

f_1

w_0

w_1

f_2

f_3

f_4

w_2

w_3

\frac{\partial y}{\partial x}=

\frac{\partial f_1}{\partial x}

\frac{\partial f_2}{\partial f_1}

\frac{\partial f_4}{\partial f_2}

\frac{\partial y}{\partial f_4}

\frac{\partial f_1}{\partial x}

\frac{\partial f_3}{\partial f_1}

\frac{\partial f_4}{\partial f_3}

\frac{\partial y}{\partial f_4}

Forward Mode:

a^l=W^lh^{l-1}+b^l

h^l=\Phi(a^l)

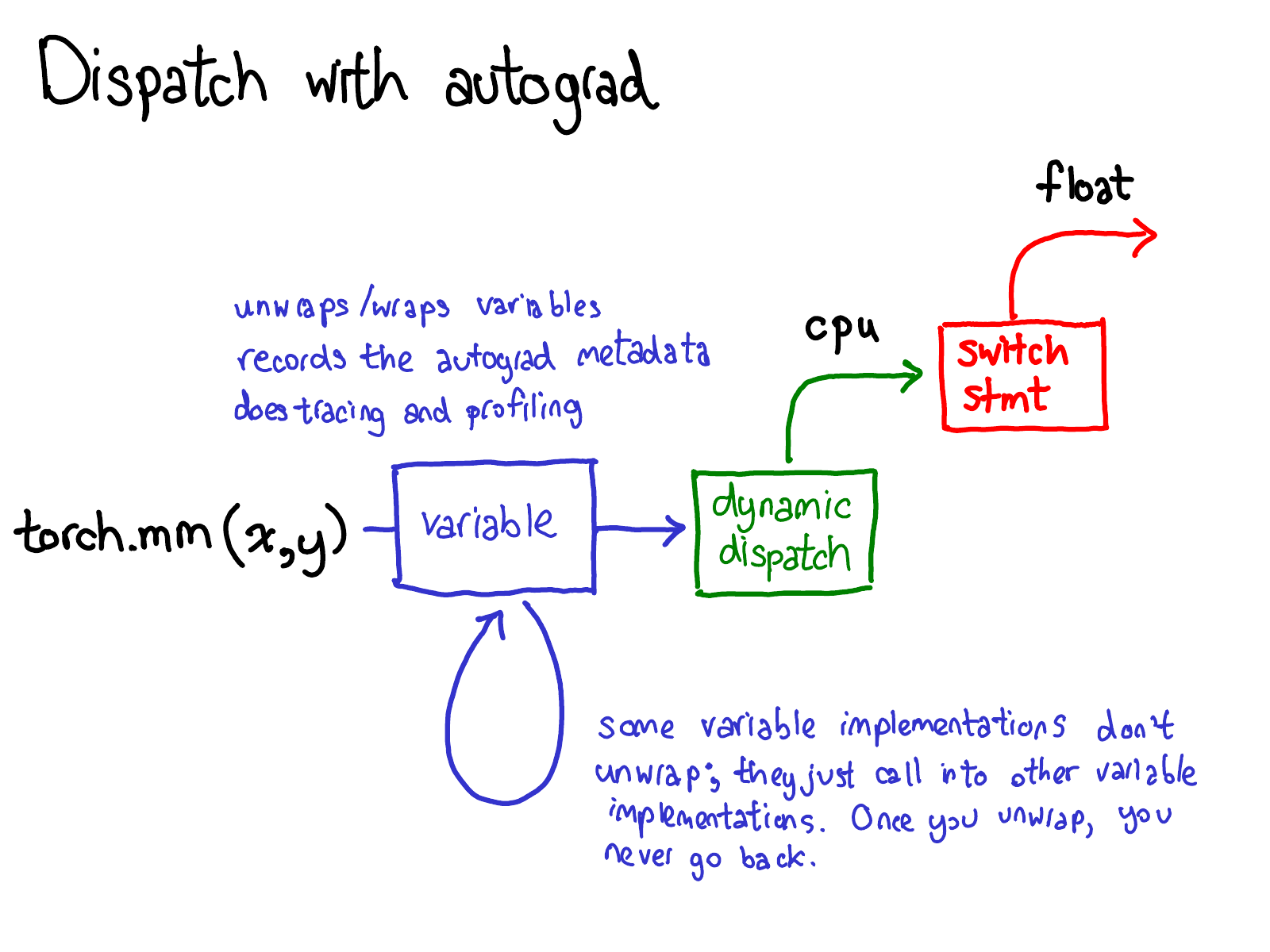
We have only two operations in the entire neural network: Multiply and Add

1. Matrix Multiplication

2. Element-wise addition and (non-linear) transformation

What if some functions or operators that I am looking for is not there in the PyTorch?

Implement forward and backward pass in the autograd.Functions and check the implementation with autograd.gradcheck (finite diff computation).

If you are sure that your function can not be create using composite function (combination of functions and operators that exist already), then you have to write your own.

torch.nn.Module

Developing Deep Learning Models using

Pytorch

Arun Prakash A

DL Course Instructor

BS, IIT Madras, POD

# parameter initialization
W1 = torch.randn(size=(10,2), requires_grad=True)
b1 = torch.randn(size=(10,1), requires_grad=True)
....
for i in range(epochs):
    #forward prop  
  for i in range(len(X)):
    a1 = torch.matmul(W1,X[(i,),:].T)+b1 
    h1 = torch.sigmoid(a1)
    a2 = torch.matmul(W2,h1)+b2
    h2 = torch.sigmoid(a2)
    a3 = torch.matmul(W3,h2)+b3
    y_hat = torch.sigmoid(a3)
    #Loss function
    L = (1/1000)*torch.pow((y_hat-y[i]),2) 
    acc_loss += L.detach().item()
    
    # backprop
    L.backward() 
    
	# Optimizer
  with torch.no_grad():
    W1  -= eta*W1.grad   
    b1  -= eta*b1.grad  
    ...
 
  W1.grad.zero_()
  b1.grad.zero_()
 ...

We can see five sections of code here,

1.Parameter Initialization

2. Forward Propagation

3.Loss function

4. Backprop

5.Optimization

Which section(s) can be automated?

Given a few info, you can construct the rest..?

Module in pytorch means layers in other frameworks (of course, we are also accustomed to the latter "layers" :-))

The core steps involved in the training loop when we use the tensors alone are as follows

#Parameter initialization
w = 
b = 
for i in range(epochs):
  
  #Forward prop
  .
  .
  use suitable loss function
  # compute gradients
  
  loss.backward()
  
  # context manager
  with torch.no_grad():
    #update all parameters
    .
    use suitable optimizer 
    .
    .
  
  .zero_grad

What if we have a really big architecture with millions/billions of parameters?
What if we want to use different loss functions and optimizers for tracing/profiling?
Moving to eval() or inference mode?

x = torch.tensor()
W = torch.tensor(requires_grad=True)
b = torch.tensor(reequires_grad=True)
y = torch.matmul(W,x)+b

Layers

Given the input dim and output dim we can infer the size of parameters

Since this is one of the most frequently used operations in NN, we can wrap it around in a single block (layer) (making an abstraction out of it)

Call it a Linear Layer

This is called Modularization

Linear

Convolution

Embedding

RNN

class LinearLayer(nn.Module):

  def __init__(self,in_features,out_features):
    super(LinearLayer,self).__init__()
    self.in_features = in_features
    self.out_features = out_features
    self.w = nn.Parameter(torch.randn(in_features, out_features))
    self.b = nn.Parameter(torch.randn(out_features))

  def forward(self,x):
    out = torch.matmul(x,self.w)+self.b

Let's create a simple linear neuron with the parameters \(w,b\)

The constructor takes in arguments that are required to initialize the network (in this case, input dim and output dim)

All the variables in the base modules are initialized via a super() call.

The parameters W, b are added to the _parameter dict

The forward method has to be defined, the backprop is automated!

class Module:

  # Annotations
  training: bool
  _parameters: Dict[str, Optional[Parameter]]
  _buffers: Dict[str, Optional[Tensor]]
  _non_persistent_buffers_set: Set[str]
  _backward_pre_hooks: Dict[int, Callable]
  _backward_hooks: Dict[int, Callable]
  _is_full_backward_hook: Optional[bool]
  _forward_hooks: Dict[int, Callable]
  _forward_hooks_with_kwargs: Dict[int, bool]
  _forward_pre_hooks: Dict[int, Callable]    
  _forward_pre_hooks_with_kwargs: Dict[int, bool]
  _state_dict_hooks: Dict[int, Callable]
  _load_state_dict_pre_hooks: Dict[int, Callable]
  _state_dict_pre_hooks: Dict[int, Callable]
  _load_state_dict_post_hooks: Dict[int, Callable]
  _modules: Dict[str, Optional['Module']]

Base class

Observe that almost all the state variables (including parameters) are stored in dictionaries (make sense)

class Module:
  
  def __init__(self):
    
    torch._C._log_api_usage_once("python.nn_module")
    
    super().__setattr__('training', True)
    super().__setattr__('_parameters', OrderedDict())
    super().__setattr__('_buffers', OrderedDict())
    super().__setattr__('_non_persistent_buffers_set', set())
    super().__setattr__('_backward_pre_hooks', OrderedDict())
    super().__setattr__('_backward_hooks', OrderedDict())
    super().__setattr__('_is_full_backward_hook', None)
    super().__setattr__('_forward_hooks', OrderedDict())
    super().__setattr__('_forward_hooks_with_kwargs', OrderedDict())
    super().__setattr__('_forward_pre_hooks', OrderedDict())
    super().__setattr__('_forward_pre_hooks_with_kwargs', OrderedDict())
    super().__setattr__('_state_dict_hooks', OrderedDict())
    super().__setattr__('_state_dict_pre_hooks', OrderedDict())
    super().__setattr__('_load_state_dict_pre_hooks', OrderedDict())
    super().__setattr__('_load_state_dict_post_hooks', OrderedDict())
    super().__setattr__('_modules', OrderedDict())

Base class

Using ordered dict is a right choice (why does order matter here?)

CNN for Image classification

- TorchData

Developing Deep Learning Models using

Pytorch

Arun Prakash A

DL Course Instructor

BS, IIT Madras, POD

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

N samples

in a storage

What we have so far

torch.tensor

Torch.nn.module

(Linear, Conv2D,

RNN)

torch.optim

.Step

We could build any deep learning model with these modules

torch.nn.Parameter

torch.autograd

\theta,\nabla \theta

\theta-\nabla \theta

How do we feed in the data to the mode for training?

We can slice the batch and iterate, not a big deal

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

N samples

in a storage

1
10
5
4
3
6
17
8
9
2
11
16
13
14
15
12
7
18

Shuffled indices

Model Under

training

We can't fetch the next set of batches simultaneously when the model is being trained

Fetch

(Model waits until samples are fetched)

This is due to pythons GIL

Then, what is the purpose of TorchData?

# Load entire dataset
X, y = torch.load('some_training_set_with_labels.pt')

# Train model
for epoch in range(max_epochs):
    for i in range(n_batches):
        # Local batches and labels
        local_X, local_y = X[i*n_batches:(i+1)*n_batches,], y[i*n_batches:(i+1)*n_batches,]

        # Your model
        [...]

Could you think of some drawbacks of loading data in this way?

Especially, putting the model and data loading into the same loop

Source

Overloads Memory by (unnecessarily) loading all sample

The model waits for some time to get it samples (due to pythons GIL)

Data processing is a complex task (especially for NLP)

It involves tasks like Pre-processing (transforming), collating into batches, distributing across machines...

Having a separate module(functions) to do them makes code clean and neat.

TorchData module does that exactly with the help of `dataset` (datapipe in beta stage) and `dataloader` classes

Moreover, we do not want to transform all samples in the dataset all at once (otherwise, consumes a lot of memory)

Dataset: Map Style

We need to inherit the abstract class from `torch.utils.data.Dataset` and must implement a `getitem` and `len` method that returns a single sample from the dataset

class Dataset():
  
  def __getitem__(self, index) :
        raise NotImplementedError

  def __add__(self, other) :
      return ConcatDataset([self, other])

class MyDataset(Dataset):
  
  def __init__(self,path_to_dataset):
    self.path = 'path_to_dataset'
    
  def __getitem__(self, index) :
       # Load data using appropriate library
       .
       #Preprocess - transform
       #
       return a_single_sample, label

  def __add__(self, other) :
      # implement how to concatenate
      # else default will be considered
      return ConcatDataset([self, other])

We call it map because it maps an indices/keys (idx) to samples. This is suitable if you have an off-line (stored in disk) dataset. That is, all samples are available at once

What if my data is of online (streaming)? possibly coming from multiple streams

Dataset: iterable- Style

From doc:

" This type of datasets is particularly suitable for cases where random reads are expensive or even improbable, and where the batch size depends on the fetched data."

Natural Language Processing

" This course contents are well organised"

Recurrent Neural Network

[{Label:'Positive', Score:0.997}]

" The course contents are well organized"

Recurrent Neural Network

[{Label:'Positive', Score:0.997}]

Tokenize

[The, course,contents,are,well,organized]

Numericalize

[{The:10, course:18,contents:14,are:100,well:9,organized:6982}]

Embedding

[random initialization, word2vec, glove, fasttext..]

Corpora - Token

Corpus: collections of raw text (in ASCII or UTF-8)

A sequence of characters (bytes)

Group them into contiguous units called tokens (ex, words, numeric seq, punctuations)

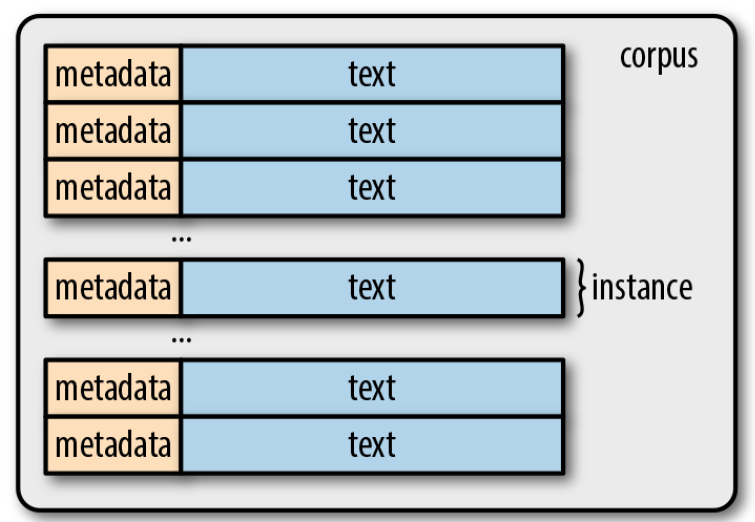
Tokenization

A process that breaks text into tokens

It is a highly complicated process, task specific, arbitrary but extremely important step

Types

Unique tokens in a corpus

A set of all types in a corpus is its vocubulary (A set of all unique tokens in the text is its vocabulary or lexicon)

Words are of two types: content words and stop words (articles, prepositions..)

Corpus: {"The mouse eat the cheese.",

"The mouse is really good to use!"}

\(\mathcal{V}:\) {the, mouse,eat, cheese, is, really good, to ,use,!}

N-Grams

n-consecutive token sequences in a text (not in a vocubulary)

Unigram: {"the", "mouse", "eat", ..}

Corpus: {"The mouse eat the cheese.",

"The mouse is really good to use!"}

Corpus: {"The mouse eat the cheese.",

"The mouse is really good to use!"}

Bigram: {"the mouse", "mouse eat", "eat the", ..}

Trigram: {"the mouse eat", "mouse eat the", "eat the cheese", ..}

Character level tokens are sometimes helpful. Those tokens are subwords in a word. Say, "-ol" in methonol, ethanol

lemmas

lemmas are root forms of words

be : is,was,were

fly : flow, flowed, flying..

Often used in traditional nlp to reduce the dimension of a vector representation.

It can also be cast as a learning problem (instead of handcrafting rules).

Torchtext

All texts (samples) from a corpus

Tokenize

(basic, subword, bpe)

Build vocabulary

(tokens to indices)

from torchtext.datasets import IMDB
train_iter = IMDB(root='./data',split='train')
all_samples = list(train_iter)

from torchtext.data.utils import get_tokenizer
tokenizer = get_tokenizer(tokenizer="basic_english",language='en')

counter=Counter()
for (label,sent) in all_samples: # iterate over all samples
  counter. Update(tokenizer(sent))
v1 = vocab(counter,min_freq=1,specials=[unk_token]) #build vocabulary
v1.set_default_index(default_index)

Task: Take a sentence and return a sequence of tokens as defined by tokenizer

Task: Dictionary of tokens {token-1: frequency, token-2: frequency, ..., token_n : frequency}

Note: We count the frequency of a token, so that we can decide whether the token be a part of vocabulary based on its freq value

Now, the vocab function assigns an integer (index) to each token

We can make use of the index to create a vector representation of words or sentences in multiple ways, for example

I	am	proud	of	you	made	me
0	1	2	3	4	5	6

I am

Sentence to vector

[0,1]

you made me proud

[0,1]

Word to vector (one-hot-encoding)

[1,0,0,0,0,0,0]

made

[0,0,0,0,0,1,0]

Say, |V| = 7 as follows

Embedding Layer

Given the index \(i\) for a token, get me a vector representation \(x_i\) of size \(k\)

We need a vector representation for each token. Initially all the vectors are purely random (as we initialize the parameters)

|V| \times k

The embedding layer is just a HUGE trainable look-up table !

x_i=[0.1,-0.1,0.8,\cdots,0.35]_{1 \times k}

If we have \(|V|\) of size 1 million, and \(k=50\), then we need to learn 50 million parameters

Challenges:

1. Vocabulary changes from dataset to dataset

2. Word embeddings may not contain embedding for all words in your vocabulary

3. Therefore, we need to use embedding layer and initialize the weights for words, not in the vocabulary of pre-trained word-embeddings, randomly

Build Transformers from scratch

(using pytorch nn.module)

Arun Prakash A

IIT Madras

Encoder

def scaled_dot_product_attention(Q, K, V):
   dim_k = K.size(-1)
   scores = torch.bmm(Q, K.transpose(1, 2)) / sqrt(dim_k)
   weights = F.softmax(scores, dim=-1)
   return torch.bmm(weights, V)

Scaled Dot Product

\text{MatMul:} \ QK^T

\text{Scale}:\frac{1}{\sqrt{d_k}}

\text{Softmax}

\text{MatMul}

Scaled Dot Product

Head

W_Q

W_K

W_V

H=\{h_1,h_2,\cdots,h_T\}

Attention Head

class AttentionHead(nn.Module):
   def __init__(self, embed_dim=512, head_dim=64):
     super().__init__()
     self.q = nn.Linear(embed_dim, head_dim)
     self.k = nn.Linear(embed_dim, head_dim)
     self.v = nn.Linear(embed_dim, head_dim)
   def forward(self, hidden_state):
     attn_outputs = scaled_dot_product_attention(
     				self.q(hidden_state), 
       				self.k(hidden_state), 
       				self.v(hidden_state))
     return attn_outputs

Concatenate (:\(T \times 512\))

Linear

W_Q^8

W_K^8

W_V^8

Scaled Dot Product

Attention

W_Q^2

W_K^2

W_V^2

Scaled Dot Product

Attention

Scaled Dot Product

Attention

h_j

W_Q^1

W_K^1

W_V^1

Multi-Head Attention

class MultiHeadAttention(nn.Module):
   def __init__(self, embed_dim=512,num_head=8):
     super().__init__()    
     head_dim = embed_dim//num_heads # 512/8 = 64
     
     # create 8 heads as pytorch module using ModuleList
     self.heads = nn.ModuleList(
     [AttentionHead(embed_dim, head_dim) for _ in range(num_heads)]
     )
     self.output_linear = nn.Linear(embed_dim, embed_dim)
      
    def forward(self, hidden_state):
     x = torch.cat([h(hidden_state) for h in self.heads], dim=-1)
     x = self.output_linear(x)
     return x

enjoyed

the

movie

transformers

Encoder Layer

Feed Forward Network

Multi-Head Attention

class FeedForward(nn.Module):
  
   def __init__(self):
     super().__init__()
     self.linear_1 = nn.Linear(512, 2048)
     self.linear_2 = nn.Linear(2048, 512)
     self.gelu = nn.GELU()
     self.dropout = nn.Dropout(0.5)
    
   def forward(self, x):
     x = self.linear_1(x)
     x = self.gelu(x)
     x = self.linear_2(x)
     x = self.dropout(x)
     return x

Encoder

Feed Forward Network

Multi-Head Attention

Add & Layer Norm

class TransformerEncoderLayer(nn.Module):
  
 def __init__(self,config):
   super().__init__()
   self.layer_norm_1 = nn.LayerNorm(config.hidden_size)
   self.layer_norm_2 = nn.LayerNorm(config.hidden_size)
   self.attention = MultiHeadAttention(config)
   self.feed_forward = FeedForward(config)
    
 def forward(self, x):
   # Apply layer normalization and then copy input into query, key, value
   hidden_state = self.layer_norm_1(x)
   # Apply attention with a skip connection
   x = x + self.attention(hidden_state)
   # Apply feed-forward layer with a skip connection
   x = x + self.feed_forward(self.layer_norm_2(x))
   return x

BERT

Preparing Data

All texts (samples) from a corpus

Sentence Tokenizer, Word Tokenizer

(basic, subword, bpe)

Build vocabulary

(tokens to indices)

Step-1

Get input ids for each token in batch of (N)samples

Randomly replace tokens with <mask> token

Pad tokens for batching samples in data loader

Ensure all samples are of same length by padding <pad> token ids

dtype: list

dtype: list

dtype: tensor