Classification functions in sci-kit learn
Dr. Ashish Tendulkar
Machine Learning Practice
IIT Madras
- In this week, we will study sklearn functionality for implementing classification algorithms.
- We will cover sklearn APIs for
- Specific classification algorithms for least square classification, perceptron, and logistic regression classifier.
- with regularization
- multiclass, multilabel and multi-output setting
- Various classification metrics.
- Specific classification algorithms for least square classification, perceptron, and logistic regression classifier.
-
Cross validation and hyper parameter search for classification works exactly like how it works in regression setting.
- However there are a couple of CV strategies that are specific to classification
Part I: sklearn API for classification
- Logistic regression
- Perceptron
- Ridge classifier (for LSC)
- K-nearest neighbours (KNNs)
- Support vector machines (SVMs)
- Naive Bayes
There are broadly two types of APIs based on their functionality:
Specific
Generic
- SGD classifier
Uses gradient descent for opt
Specialized solvers for opt
Need to specify loss function
All sklearn estimators for classification implement a few common methods for model training, prediction and evaluation.
Model training
fit(X, y[, coef_init, intercept_init, …])
Prediction
predict(X)
decision_function(X)
predicts class label for samples
predicts confidence score for samples.
Evaluation
score(X, y[, sample_weight])
Return the mean accuracy on the given test data and labels.
There a few common miscellaneous methods as follows:
get_params([deep])
gets parameter for this estimator.
converts coefficient matrix to dense array format.
set_params(**params)
densify()
sparsify()
sets the parameters of this estimator.
converts coefficient matrix to sparse format.
Now let's study how to implement different classifiers with sklearn APIs.
Let's start with implementation of least square classification (LSC) with RidgeClassifier API.
Ridge classifier
- treated as multi-output regression
- predicted class corresponds to the output with the highest value
- classifier first converts binary targets to {-1, 1} and then treats the problem as a regression task, optimizing the objective of regressor:
Binary classification:
Multiclass classification:
- minimize a penalized residual sum of squares
-
\(\min\limits_\mathbf w ||\mathbf{Xw}-\mathbf{y}||_2^2 + \alpha ||\mathbf w||_2^2\)
- sklearn provides different solvers for this optimization
- sklearn uses \(\alpha\) to denote regularization rate
- predicted class corresponds to the sign of the regressor’s prediction
-
\(\min\limits_\mathbf w ||\mathbf{Xw}-\mathbf{y}||_2^2 + \alpha ||\mathbf w||_2^2\)
How to train a least square classifier?
Step 1: Instantiate a classification estimator without passing any arguments to it. This creates a ridge classifier object.
from sklearn.linear_model import RidgeClassifier
ridge_classifier = RidgeClassifier()Step 2: Call fit method on ridge classifier object with training feature matrix and label vector as arguments.
Note: The model is fitted using X_train and y_train.
# Model training with feature matrix X_train and
# label vector or matrix y_train
ridge_classifier.fit(X_train, y_train)How to set regularization rate in RidgeClassifier?
Set alpha to float value. The default value is 0.1.
- alpha should be positive.
- Larger alpha values specify stronger regularization.
from sklearn.linear_model import RidgeClassifier
ridge_classifier = RidgeClassifier(alpha=0.001)How to solve optimization problem in RidgeClassifier?
Using one of the following solvers
svd
cholesky
sparse_cg
lsqr
sag , saga
uses a Singular Value Decomposition of the feature matrix to compute the Ridge coefficients.
lbfgs
uses scipy.linalg.solve function to obtain the closed-form solution
uses the conjugate gradient solver of scipy.sparse.linalg.cg .
uses the dedicated regularized least-squares routine scipy.sparse.linalg.lsqr and it is fastest.
uses a Stochastic Average Gradient descent iterative procedure
'saga' is unbiased and more flexible version of 'sag'
uses L-BFGS-B algorithm implemented in scipy.optimize.minimize .
can be used only when coefficients are forced to be positive.
Uses of solver in RidgeClassifier
- For large scale data, use '
sparse_cg' solver.
-
When both
n_samplesandn_featuresare large, use ‘sag’ or ‘saga’ solvers.-
Note that fast convergence is only guaranteed on features with approximately the same scale.
-
How to make RidgeClassifier select the solver automatically?
auto
chooses the solver automatically based on the type of data
ridge_classifier = RidgeClassifier(solver=auto) if solver == 'auto':
if return_intercept:
# only sag supports fitting intercept directly
solver = "sag"
elif not sparse.issparse(X):
solver = "cholesky"
else:
solver = "sparse_cg"Default choice for solver is auto .
If data is already centered, set fit_intercept as false, so that no intercept will be used in calculations.
Is intercept estimation necessary for RidgeClassifier?
ridge_classifier = RidgeClassifier(fit_intercept=True)Default:
How to make predictions on new data samples?
Use predict method to predict class labels for samples
# Predict labels for feature matrix X_test
y_pred = ridge_classifier.predict(X_test)Other classifiers also use the same predict method.
Step 2: Call predict method on classifier object with feature matrix as an argument.
Step 1: Arrange data for prediction in a feature matrix of shape (#samples, #features) or in sparse matrix format.
RidgeClassifierCV implements RidgeClassifier with built-in cross validation.
Let's implement perceptron classifier with Perceptron API.
-
It is a simple classification algorithm suitable for large-scale learning.
Perceptron classification
-
Shares the same underlying implementation with
SGDClassifier
Perceptron uses SGD for training.
Perceptron()
SGDClassifier(loss="perceptron", eta0=1, learning_rate="constant", penalty=None)
How to implement perceptron classifier?
Step 1: Instantiate a Perceptron estimator without passing any arguments to it to create a classifier object.
from sklearn.linear_model import Perceptron
perceptron_classifier = Perceptron()Step 2: Call fit method on perceptron estimator object with training feature matrix and label vector as arguments.
# Model training with feature matrix X_train and
# label vector or matrix y_train
perceptron_classifier.fit(X_train, y_train)Perceptron can be further customized with the following parameters:
penalty
(default = 'l2')
alpha
(default = 0.0001)
l1_ratio
(default = 0.15)
fit_intercept
(default = True)
max_iter
(default = 1000)
tol
(default = 1e-3)
eta0
(default = 1)
early_stopping
(default = False)
validation_fraction
(default = 0.1)
n_iter_no_change
(default = 5)
- Perceptron classifier can be trained in an iterative manner with partial_fit method
- Perceptron classifier can be initialized to the weights of the previous run by specifying warm_start = True in the constructor.
Let's implement logistic regression classifier with LogisticRegression API.
LogisticRegression API
- Implements logistic regression classifier, which is also known by a few different names like logit regression, maximum entropy classifier (maxent) and log-linear classifier.
- This implementation can fit
- binary classification
- one-vs-rest (OVR)
- multinomial logistic regression
- Provision for \(\ell_1,\ell_2\) or elastic-net regularization
How to train a LogisticRegression classifier?
Step 1: Instantiate a classifier estimator without passing any arguments to it. This creates a logistic regression object.
from sklearn.linear_model import LogisticRegression
logit_classifier = LogisticRegression()Step 2: Call fit method on logistic regression classifier object with training feature matrix and label vector as arguments
# Model training with feature matrix X_train and
# label vector or matrix y_train
logit_classifier.fit(X_train, y_train)Logistic regression uses specific algorithms for solving the optimization problem in training. These algorithms are known as solvers.
The choice of the solver depends on the classification problem set up such as size of the dataset, number of features and labels.
How to select solvers for Logistic Regression classifier?
solver
- For small datasets, ‘liblinear’ is a good choice, whereas ‘sag’ and ‘saga ’ are faster for large ones.
- For multiclass problems, only ‘
newton-cg’, ‘sag’, ‘saga’ and ‘lbfgs’ handle multinomial loss. - ‘
liblinear’ is limited to one-versus-rest schemes
‘newton-cg ’
‘lbfgs ’
‘liblinear ’
‘sag
‘saga ’
logit_classifier = LogisticRegression(solver='lbfgs')- For unscaled datasets, ‘
liblinear', 'lbfgs' and 'newton-cg' are robust.
By default, logistic regression uses lbfgs solver.
How to add regularization in Logistic Regression classifier?
Regularization is applied by default because it improves numerical stability.
penalty
- \(l2\) - adds a L2 penalty term
- \(l1\) - adds a L1 penalty term
- elasticnet - both L1 and L2 penalty terms are added
- none - no penalty is added
logit_classifier = LogisticRegression(penalty='l2')By default, it uses L2 penalty.
- Not all the solvers supports all the penalties.
-
Select appropriate solver for the desired penalty.
-
L2 penalty is supported by all solvers
-
L1 penalty is supported only by a few solvers.
-
| Solver | Penalty |
|---|---|
‘newton-cg ’ |
[‘l2’, ‘none’] |
‘lbfgs ’ |
[‘l2’, ‘none’] |
‘liblinear’ |
[‘l1’, ‘l2’] |
‘sag’ |
[‘l2’, ‘none’] |
‘saga ’ |
[‘elasticnet’, ‘l1’, ‘l2’, ‘none’] |
How to control amount of regularization in logistic regression?
- sklearn implementation uses parameter C, which is inverse of regularization rate to control regularization.
- Recall
- C is specified in the constructor and must be positive
- Smaller value leads to stronger regularization.
- Larger value leads to weaker regularization.
LogisticRegression classifier has a class_weight parameter in its constructor.
What purpose does it serve?
Exercise: Read stack overflow discussion on this parameter.
- Handles class imbalanace with differential class weights.
- Mistakes in a class are penalized by the class weight.
- Higher value here would mean higher emphasis on the class.
This parameter is available in classifier estimators in sklearn.
LogisticRegressionCV implements logistic regression with in built cross validation support to find the best values of C and l1_ratio parameters according to the specified scoring attribute.
These classifiers can also be implemented with a generic SGDClassifier API by setting the loss parameter appropriately.
Let's study SGDClassifier API.
- SGD is a simple yet very efficient approach to fitting linear classifiers under convex loss functions
SGDClassifier
- This API uses SGD as an optimization technique and can be applied to build a variety of linear classifiers by adjusting the loss parameter.
-
Easily scales up to large scale problems with more than \(10^5\) training examples and \(10^5\) features. It also works with sparse machine learning problems
- Text classification and natural language processing
- It supports multi-class classification by combining multiple binary classifiers in a “one versus all” (OVA) scheme.
We need to set loss parameter appropriately to build train classifier of our interest with SGDClassifier
loss parameter
'hinge' - (soft-margin) linear Support Vector Machine
'modified_huber' - smoothed hinge loss brings tolerance to outliers as well as probability estimates
'log' - logistic regression
'squared_hinge' - like hinge but is quadratically penalized
'perceptron' - linear loss used by the perceptron algorithm
‘squared_error’, ‘huber’, ‘epsilon_insensitive’, or ‘squared_epsilon_insensitive’ - regression losses
By default SGDClassifier uses hinge loss and hence trains linear support vector machine classifier.
SGDClassifier(loss='log')
LogisticRegression(solver='sgd')
SGDClassifier(loss='hinge')
Linear Support vector machine
- An instance of SGDClassifier might have an equivalent estimator in the scikit-learn API.
How does SGDClassifier work?
- SGDClassifier implements a plain stochastic gradient descent learning routine.
- the gradient of the loss is estimated with one sample at a time and the model is updated along the way with a decreasing learning rate (or strength) schedule.
Advantages:
- Efficiency.
- Ease of implementation
Disadvantages:
- Requires a number of hyperparameters.
- Sensitive to feature scaling.
-
It is important
- to permute (shuffle) the training data before fitting the model.
- to standardize the features.
How to use SGDClassifier for training a classifer?
Step 1: Instantiate a SGDClassifer estimator by setting appropriate loss parameter to define classifier of interest. By default it uses hinge loss, which is used for training linear support vector machine.
from sklearn.linear_model import SGDClassifier
SGD_classifier = SGDClassifier(loss='log')Step 2: Call fit method on SGD classifier object with training feature matrix and label vector as arguments.
# Model training with feature matrix X_train and
# label vector or matrix y_train
SGD_classifier.fit(X_train, y_train)Here we have used `log` loss that defines a logistic regression classifier.
How to perform regularization in SGD classifier?
penalty
- \(l2\) - adds a L2 penalty term
- \(l1\) - adds a L1 penalty term
- elasticnet - Convex combination of L2 and L1
(1 - l1_ratio) * L2 + l1_ratio * L1
SGD_classifier = SGDClassifier(penalty='l2')(l1_ratio controls the convex combination of L1 and L2 penalty. default=0.15)
Default:
- Constant that multiplies the regularization term.
- Has float values and default = 0.0001
alpha
How to set maximum number of epochs for SGD Classifier?
SGD_classifier = SGDClassifier(max_iter=100)Default:
max_iter = 1000
The maximum number of passes over the training data (aka epochs) is an integer that can be set by the max_iter parameter.
Some common parameters between SGDClassifier and SGDRegressor
learning_rate
Stopping criteria
warm_start
‘constant’
‘optimal’
‘invscaling’
‘adaptive’
average
- SGDClassifier also supports averaged SGD (ASGD)
‘True’
‘False’
tol
n_iter_no_change
max_iter
early_stopping
validation_fraction
Summary
We learnt how to implement the following classifiers with sklearn APIs:
- Least square classification (RidgeClassifier)
- Perceptron (Perceptron)
- Logistic regression (LogisticRegression)
Alternatively we can use SGDClassifier with appropriate loss setting for implementing these classifiers:
- loss = `log` for logistic regression
- loss = `perceptron` for perceptron
- loss = `squared_error` for least square classification
Classification estimators implements a few common methods like fit, score, decision_function, and predict.
- These estimators can be readily used in multiclass setting.
- They support regularized loss function optimization.
- All classification estimators have ability to deal with class imbalance through class_weight parameter in the constructor.
Part II: Multi-learning classification set up
Let's extend these classifiers to multi-learning (multi-class, multi-label & multi-output) settings.
Basics of multiclass, multilabel and multioutput classification
- Multiclass classification has exactly one output label and the total number of labels > 2.
- For more than one output, there are two types of classification models:
Multilabel
total #labels = 2
Multiclass multioutput
total #labels > 2
We will refer both these models as multi-label classification models, where # of output labels > 1.
Multiclass, multilabel, multioutput problems are referred to as multi-learning problems.
Multiclass classification
(sklearn.multiclass)
Multilabel classification
(sklearn.multioutput)
problem types
meta-estimators
OneVsOneClassifier
OneVsRestClassifier
OutputCodeClassifier
MultiOutputClassifier
ClassifierChain
- sklearn provides a bunch of meta-estimators, which extend the functionality of base estimators to support multi-learning problems.
- The meta-estimators transform the multi-learning problem into a set of simpler problems and fit one estimator per problem.
- Many sklearn estimators have built-in support for multi-learning problems.
- Meta-estimators are not needed for such estimators, however meta-estimators can be used in case we want to use these base estimators with strategies beyond the built-in ones.
Inherently multiclass
Multiclass as OVO
Multiclass as OVR
Multilabel
Inherently multiclass
Multilabel
LogisticRegression (multi_class = 'multinomial')
RidgeClassifier
LogisticRegressionCV (multi_class = 'multinomial')
RidgeClassifierCV
Multiclass as OVR
Perceptron
LogisticRegression (multi_class = 'ovr')
SGDClassifier
LogisticRegressionCV (multi_class = 'ovr')
RidgeClassifier
RidgeClassifierCV
First we will study multiclass APIs in sklearn.
Multi-class classification
- Classification task with more than two classes.
- Each example is labeled with exactly one class
In Iris dataset,
- There are three class labels: setosa, versicolor and virginica.
- Each example has exactly one label of the three available class labels.
- Thus, this is an instance of a multi-class classification.
In MNIST digit recognition dataset,
- There are 10 class labels: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
- Each example has exactly one label of the 10 available class labels.
- Thus, this is an instance of a multi-class classification.
How to represent class labels in multi-class setup?
- Use LabelBinarizer transformation to convert the class label to multi-class format.
- Each example is marked with a single label out of k labels. The shape of label vector is \((n, 1)\).
- The resulting label vector has shape of \((n, k)\).
from sklearn.preprocessing import LabelBinarizer
y = np.array(['apple', 'pear', 'apple', 'orange'])
y_dense = LabelBinarizer().fit_transform(y)[[1 0 0] [0 0 1] [1 0 0] [0 1 0]]
Let's say, you are given labels as part of the training set, how do we check if they are is suitable for multi-class classification?
- Use type_of_target to determine the type of the label.
from sklearn.utils.multiclass import type_of_target
type_of_target(y)- In case, \(y\) is a vector with more than two discrete values, type_of_target returns multiclass.
type_of_target can determine different types of multi-learning targets.
target_type
‘multiclass’
‘multiclass-multioutput’
‘unknown’
y
- contains more than two discrete values
- not a sequence of sequences
- 1d or a column vector
- array-like but none of the above, such as a 3d array,
- sequence of sequences, or an array of non-sequence objects.
- 2d array that contains more than two discrete values
- not a sequence of sequences
- dimensions are of size > 1
‘multilabel-indicator’
- label indicator matrix
- an array of two dimensions with at least two columns, and at most 2 unique values.
Examples
>>> type_of_target([1, 0, 2])
'multiclass'
>>> type_of_target([1.0, 0.0, 3.0])
'multiclass'
>>> type_of_target(['a', 'b', 'c'])
'multiclass'>>> type_of_target(np.array([[1, 2], [3, 1]]))
'multiclass-multioutput'multiclass
multiclass-multioutput
multilabel-indicator
type_of_target(np.array([[0, 1], [1, 1]]))
'multilabel-indicator'
>>> type_of_target([[1, 2]])
'multilabel-indicator'Apart from these, there are three more types, type_of_target can determine targets corresponding to regression and binary classification.
- continuous - regression target
- continuous-multioutput - multi-output target
- binary - classification
All classifiers in scikit-learn perform multiclass classification out-of-the-box.
- Use sklearn.multiclass module only when you want to experiment with different multiclass strategies.
- Using different multi-class strategy than the one implemented by default may affect performance of classifier in terms of either generalization error or computational resource requirement.
What are different multi-class classification strategies implemented in sklearn?
- One-vs-all or one-vs-rest (OVR)
- One-vs-One (OVA)
- OVR is implemented by OneVsRestClassifier API.
- OVA is implemented by OneVsOneClassifier API.
OVR - OneVsRestClassifier
- Fits one classifier per class \(c\) - \(c \text{ vs } \text{ not }c\).
- This approach is computationally efficient and requires only \(k\) classifiers.
- The resulting model is interpretable.
OneVsRest classifier also supports multilabel classification. We need to supply labels as indicator matrix of shape \((n, k)\).
from sklearn.multiclass import OneVsRestClassifier
OneVsRestClassifier(LinearSVC(random_state=0)).fit(X, y)- We need to supply estimator as an argument in the constructor.
- Support methods like other classifiers - fit, predict, predict_proba, partial_fit.
OVA - OneVsOneClassifier
- Fits one classifier per pair of classes. Total classifiers = \(k \choose 2\).
- Predicts class that receives maximum votes.
- The tie among classes is broken by selecting the class with the highest aggregate classification confidence.
OneVsOne classifier processes subset of data at a time and is useful in cases where the classifier does not scale with the data.
from sklearn.multiclass import OneVsOneClassifier
OneVsOneClassifier(LinearSVC(random_state=0)).fit(X, y)- We need to supply estimator as an argument in the constructor.
- Support methods like other classifiers - fit, predict, predict_proba, partial_fit.
What is the difference between OVR and OVA?
OneVsRestClassifier
OneVsOneClassifier
- Fits one classifier per class.
- For each classifier, the class is fitted against all the other classes.
-
Fits one classifier per pair of classes.
-
At prediction time, the class which received the most votes is selected.
Now we will learn how to perform multilabel and multi-output classification.
How MultiOutputClassifier works?
- Strategy consists of fitting one classifier per target.
- Allows multiple target variable classifications.
Input Feature Matrix (X)
Classifier #1
Classifier #2
Classifier #k
Class #1
Class #2
Class #k
How ClassifierChain works?
- A multi-label model that arranges binary classifiers into a chain.
- Way of combining a number of binary classifiers into a single multi-label model.
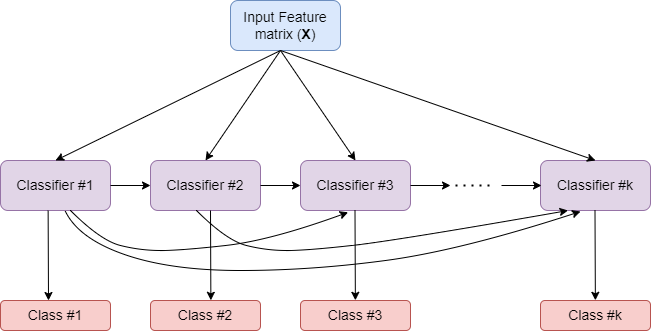
Comparison of MultiOutputClassifier and ClassifierChain
MultiOutputClassifier
ClassifierChain
- Allows multiple target variable classifications.
- Able to estimate a series of target functions that are trained on a single predictor matrix to predict a series of responses.
- For a multi-label classification problem with \(k\) classes, \(k\) binary classifiers are assigned an integer between 0 and \(k-1\).
- These integers define the order of models in the chain.
- Capable of exploiting correlations among targets.
Summary
- Different types of multi-learning setups: multi-class, multi-label, multi-output.
- type_of_target to determine the nature of supplied labels.
- Meta-estimators:
- multi-class: One-vs-rest, one-vs-one
- multi-label: Classifier chain and multi-output classifier
Evaluating Classifiers
So far we learnt how to train classifiers for binary, multi-class and multi-label/output cases.
We will learn how to evaluate these classifiers with different scoring functions and with cross-validation.
We will also study how to set hyper-parameters for classifiers.
Many cross-validation and HPT methods discussed in the regression context are also applicable in classifiers.
- We will not repeat that discussion in this topic.
- Instead we will focus on only additional methods that are specific to classifiers.
There may be issues like class imbalance in classification, which tend to impact the cross validation folds.
The overall class distribution and the ones in folds may be different and this has implications in effective model training.
sklearn.model_selection module provides three stratified APIs to create folds such that the overall class distribution is replicated in individual folds.
Stratified cross validation iterators
sklearn.model_selection module provides the following three stratified APIs to create folds such that the overall class distribution is replicated in individual folds.
- StratifiedKFold
- RepeatedStratifiedKFold
- StratifiedShuffleSplit
Note: Folds obtained via StratifiedShuffleSplit may not be completely different.
LogisticRegressionCV
- Support in-build cross validation for optimizing hyperparameters
- The following are key parameters for HPT and cross validation
cv specifies cross validation iterator
scoring specifies scoring function to use for HPT
cs specifies regularization strengths to experiment with.
- Choosing the best hyper-parameters
refit = True
refit = False
Scores averaged across folds, values corresponding to the best score are selected and final refit with these parameters
the coefs, intercepts and C that correspond to the best scores across folds are averaged.
Now let's look at classification metrics implemented in sklearn.
sklearn.metrics implements a bunch of classification scoring metrics based on true labels and predicted labels as inputs.
accuracy_score
balanced_accuracy_score
top_k_accuracy_score
roc_auc_score
precision_score
recall_score
f1_score
score(actual_labels, predicted_labels)
Classification metrics
Confusion matrix
-
confusion_matrixevaluates classification accuracy by computing the confusion matrix with each row corresponding to the true class.
from sklearn.metrics import confusion_matrix
confusion_matrix(y_true, y_predicted)Entry \(i,j\) in a confusion matrix
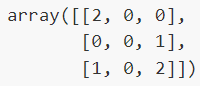
Example:
number of observations actually in group \(i\), but predicted to be in group \(j\).
Confusion matrix can be displayed with ConfusionMatrixDisplay API in sklearn.metrics.
- Confusion matrix
- From estimators
- From predictions
ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=clf.classes_)ConfusionMatrixDisplay.from_estimator(clf, X_test, y_test)ConfusionMatrixDisplay.from_predictions(y_test, y_pred)The classification_report function builds a text report showing the main classification metrics.
from sklearn.metrics import classification_report
print(classification_report(y_true, y_predicted))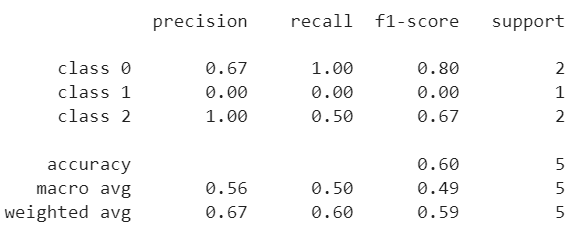
Classifier Performance across probability thresholds
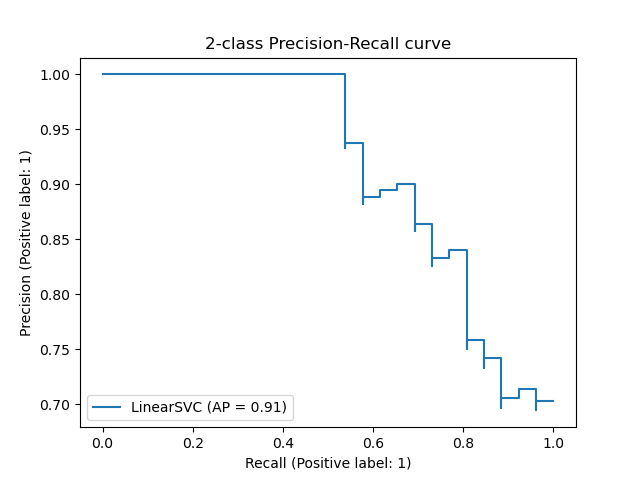
from sklearn.metrics import precision_recall_curve
precision, recall, thresholds = precision_recall_curve(y_true, y_predicted)from sklearn.metrics import roc_curve
fpr, tpr, thresholds = metrics.roc_curve(y_true, y_scores, pos_label=2)How to extend binary metric to multiclass or multilabel problems?
- Treat data as a collection of binary problems, one for each class.
- Then, average binary metric calculations across the set of classes.
-
Can be done using
averageparameter.
calculates the mean of the binary metrics
computes the average of binary metrics in which each class’s score is weighted by its presence in the true data sample.
gives each sample-class pair an equal contribution to the overall metric
calculates the metric over the true and predicted classes for each sample in the evaluation data, and returns their average
returns an array with the score for each class
macro
weighted
micro
samples
None
Summary
- Classification specific cross validation iterator based on stratification.
- Classification metrics
- Extending binary metrics to multi-learning set up.