Deep Learning Practice - NLP
Tokenisation, HF Tokenizers
Mitesh M. Khapra
AI4Bharat, Department of Computer Science and Engineering, IIT Madras
N \times
Recall that the transformer is a simple encoder-decoder model with attention mechanism at its core
The input is a sequence of words in the source language
The output is also a sequence of words in the target language
Source Input Sequence
Target Input Sequence
Predicted Output Sequence
Multi-Head Attention
Feed forward NN
Add&Norm
Add&Norm
Multi-Head cross Attention
Feed forward NN
Add&Norm
Add&Norm
Multi-Head Masked Attention
Add&Norm
I am reading a book
Naan oru puthagathai padiththu kondirukiren
The lengths of the input and output sequences need not be the same
The tokenizer simply splits the input sequence into tokens.
Each token is associated with a unique ID.
A simple approach is to use whitespace for splitting the text.
Tokenizer
Token to ID
embeddings
Language Model
ID to token
How are you?
\{How,are, you\}
\{How:1,\\
are:2, \\
you:3\}
1:[0.1,0.35 \cdots,0.08],\\
2:[0.01,1.00,\cdots,0.8], \\
3:[0.12,0.00,\cdots,0.46]\\
Tokenizer in the Training pipeline
The model then takes these embeddings and predicts token IDs.
Each ID is associated with a unique embedding vector.
During inference, the predicted token IDs are converted back to tokens (and then to words).
token to words
The tokenizer simply splits the input sequence into tokens.
A simple approach is to use whitespace for splitting the text.
Tokenizer in the Training pipeline
The tokenizer essentially contains two components: the encoder, which converts input word (token) to a token id, and the decoder, which performs the reverse operation.
Tokenizer
Token ID
embeddings
Language Model
ID to token
How are you?
\{How,are, you\}
\{How:1,\\
are:2, \\
you:3\}
1:[0.1,0.35 \cdots,0.08],\\
2:[0.01,1.00,\cdots,0.8], \\
3:[0.12,0.00,\cdots,0.46]\\
token to words
Encoder
Decoder
Each token is associated with a unique ID.
The model then takes these embeddings and predicts token IDs.
Each ID is associated with a unique embedding vector.
During inference, the predicted token IDs are converted back to tokens (and then to words).
Tokenizer in the Training pipeline
The size of the vocabulary determines the size of the embedding table
Tokenizer
Token ID
embeddings
Language Model
ID to token
How are you?
\{How,are, you\}
\{How:1,\\
are:2, \\
you:3\}
1:[0.1,0.35 \cdots,0.08],\\
2:[0.01,1.00,\cdots,0.8], \\
3:[0.12,0.00,\cdots,0.46]\\
token to words
The question then is how do we build (learn) a vocabulary \(\mathcal{V}\) from a large corpus that contains billions of sentences?
We can split the text into words using whitespace (now called pre-tokenization) and add all unique words in the corpus to the vocabulary.
We also include special tokens such as <go>,<stop>,<mask>,<sep>,<cls> and others to the vocabulary based on the type of downstream tasks and the architecture (GPT/BERT) choice
Is spliting the input text into words using whitespace a good approach?
What about languages like Japanese, which do not use any word delimiters like space?
Why not treat each individual character in a language as a token in the vocabulary?
Some Questions
If so, do we treat the words "enjoy" and "enjoyed" as separate tokens?
Finally, what are good tokens?
I
enjoyed
the
movie
transformers
Feed Forward Network
Multi-Head Attention
<go>
<stop>
映画『トランスフォーマー』を楽しく見ました
Challenges in building a vocabulary
What should be the size of vocabulary?
Larger the size, larger the size of embedding matrix and greater the complexity of computing the softmax probabilities. What is the optimal size?
Out-of-vocabulary
If we limit the size of the vocabulary (say, 250K to 50K) , then we need a mechanism to handle out-of-vocabulary (OOV) words. How do we handle them?
Handling misspelled words in corpus
Often, the corpus is built by scraping the web. There are chances of typo/spelling errors. Such erroneous words should not be considered as unique words.
Open Vocabulary problem
A new word can be constructed (say,in agglutinative languages) by combining existing words . The vocabulary, in principle, is infinite (that is, names,numbers,..) which makes a task like machine translation challenging
Module 1 : Tokenization algorithms
AI4Bharat, Department of Computer Science and Engineering, IIT Madras
Mitesh M. Khapra
Wishlist
Moderate-sized Vocabulary
Efficiently handle unknown words during inference
Be language agnostic
Categories
c h a r a c t e r l e v e l
word level
sub-word level
WordPiece
SentencePiece
BytePairEncoding (BPE)
1-112
30K-50K
>250K
Vocab size
Vocab size
Vocab size
Complexities of subword tokenization [Andrej Karpathy]
-
Why can't LLMs spell words? Tokenization.
-
Why can't LLMs do super simple string processing tasks like reversing a string? Tokenization.
-
Why are LLMs not good at non-English languages (e.g. Japanese)? Tokenization.
-
Why are LLMs bad at simple arithmetic? Tokenization.
-
Why did GPT-2 have trouble coding in Python? Tokenization.
-
What is the real root of suffering? Tokenization.
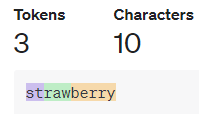
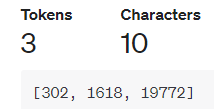
Module 1.1 : Byte Pair Encoding
AI4Bharat, Department of Computer Science and Engineering, IIT Madras
Mitesh M. Khapra
General Pre-processing steps
Hmm.., I know I Don't know
Input text
hmm.., i know i don't know
normalization
Pre-tokenization
[hmm.., i, know, i , don't,know]
Subword Tokenization
[hmm.., i, know, i, do, #n't,know]
Splitting the text by whitespace was traditionally called tokenization. However, when it is used with a sub-word tokenization algorithm, it is called pre-tokenization.
First the text is normalized, which involves operations such as treating cases, removing accents, eliminating multiple whitespaces, handling HTML tags, etc.
The input text corpus is often built by scraping web pages and ebooks.
Learn the vocabulary (called training) using these words
The tokenization schemes follow a sequence of steps to learn the vocabulary.
Text Corpus
Learn the vocabulary
Pre-process
Post-process
Model
\mathcal{V}
I enjoyed the movie
[I enjoy #ed the movie]
[I enjoy #ed the movie .]
I enjoyed the movie.
Preprocess
Algorithm
import re, collections
def get_stats(vocab):
pairs = collections.defaultdict(int)
for word, freq in vocab.items():
symbols = word.split()
for i in range(len(symbols)-1):
pairs[symbols[i],symbols[i+1]] += freq
return pairs
def merge_vocab(pair, v_in):
v_out = {}
bigram = re.escape(' '.join(pair))
p = re.compile(r'(?<!\S)' + bigram + r'(?!\S)')
for word in v_in:
w_out = p.sub(''.join(pair), word)
v_out[w_out] = v_in[word]
return v_out
vocab = {'l o w </w>' : 5, 'l o w e r </w>' : 2,
'n e w e s t </w>':6, 'w i d e s t </w>':3}
num_merges = 10
for i in range(num_merges):
pairs = get_stats(vocab)
best = max(pairs, key=pairs.get)
vocab = merge_vocab(best, vocab)
print(best)
Start with a dictionary that contains words and their counts
Append a special symbol </w> at the end of each word in the dictionary
Set required number of merges (a hyperparameter)
Get the frequency count for a pair of characters
Merge pairs with maximum occurrence
Initialize the character-frequency table (base vocabulary)
Example
knowing the name of something is different from knowing something. knowing something about everything isn't bad
| Word | Frequency |
|---|---|
| 'k n o w i n g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h i n g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h i n g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h i n g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
</w> identifies the word boundary.
Objective: Find most frequently occurring byte-pair
Example
knowing the name of something is different from knowing something. knowing something about everything isn't bad
| Word | Frequency |
|---|---|
| 'k n o w i n g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h i n g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h i n g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h i n g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
</w> identifies the word boundary.
Objective: Find most frequently occurring byte-pair
Let's count the word frequencies first.
We can count character frequencies from the table
| Word | Frequency |
|---|---|
| 'k n o w i n g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h i n g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h i n g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h i n g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
| Character | Frequency |
|---|---|
| 'k' | 3 |
Initial token count
Word count
\vdots
\vdots
We could infer that "k" has occurred three times by counting the frequency of occurrence of words having the character "k" in it.
In this corpus, the only word that contains "k" is the word "knowing" and it has occurred three times.
| Word | Frequency |
|---|---|
| 'k n o w i n g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h i n g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h i n g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h i n g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
| Character | Frequency |
|---|---|
| 'k' | 3 |
Initial token count
Word count
| Character | Frequency |
|---|---|
| 'k' | 3 |
| 'n' | 13 |
\vdots
\vdots
Vocab size:13
2*3=6
1*1=1
1*2=2
1*1=1
1*1=1
1*1=1
1*1=1
| Word | Frequency |
|---|---|
| 'k n o w i n g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h i n g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h i n g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h i n g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
| Character | Frequency |
|---|---|
| 'k' | 3 |
Initial token count
Word count
| Character | Frequency |
|---|---|
| 'k' | 3 |
| 'n' | 13 |
| Character | Frequency |
|---|---|
| 'k' | 3 |
| 'n' | 13 |
| 'o' | 9 |
| Character | Frequency |
|---|---|
| 'k' | 3 |
| 'n' | 13 |
| 'o' | 9 |
| '</w>' | 3+1+1+1+2+...+1=16 |
\vdots
\vdots
Vocab size:13
| Word | Frequency |
|---|---|
| 'k n o w i n g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h i n g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h i n g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h i n g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
| Character | Frequency |
|---|---|
| 'k' | 3 |
Initial tokens and count
Word count
| Character | Frequency |
|---|---|
| 'k' | 3 |
| 'n' | 13 |
| Character | Frequency |
|---|---|
| 'k' | 3 |
| 'n' | 13 |
| 'o' | 9 |
| Character | Frequency |
|---|---|
| 'k' | 3 |
| 'n' | 13 |
| 'o' | 9 |
| '</w>' | 3+1+1+1+2+...+1=16 |
\vdots
\vdots
| Character | Frequency |
|---|---|
| 'k' | 3 |
| 'n' | 13 |
| 'o' | 9 |
| '</w>' | 16 |
| "'" | 1 |
\vdots
\vdots
\vdots
\vdots
Vocab size:13
Initial Vocab Size :22
| Word | Frequency |
|---|---|
| 'k n o w i n g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h i n g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h i n g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h i n g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
| Word | Frequency |
|---|---|
| ('k', 'n') | 3 |
Byte-Pair count
Word count
| Word | Frequency |
|---|---|
| 'k n o w i n g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h i n g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h i n g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h i n g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
| Word | Frequency |
|---|---|
| ('k', 'n') | 3 |
| ('n', 'o') | 3 |
Byte-Pair count
Word count
| Word | Frequency |
|---|---|
| 'k n o w i n g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h i n g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h i n g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h i n g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
| Word | Frequency |
|---|---|
| ('k', 'n') | 3 |
| ('n', 'o' | 3 |
| ('o', 'w') | 3 |
Byte-Pair count
Word count
| Word | Frequency |
|---|---|
| 'k n o w i n g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h i n g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h i n g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h i n g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
| Word | Frequency |
|---|---|
| ('k', 'n') | 3 |
| ('n', 'o' | 3 |
| ('o', 'w') | 3 |
| ('w', 'i') | 3 |
| ('i', 'n') |
Byte-Pair count
3
+2
+1
+1
=7
Word count
| Word | Frequency |
|---|---|
| 'k n o w i n g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h i n g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h i n g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h i n g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
| Word | Frequency |
|---|---|
| ('k', 'n') | 3 |
| ('n', 'o' | 3 |
| ('o', 'w') | 3 |
| ('w', 'i') | 3 |
| ('i', 'n') | 7 |
| ('n', 'g') | 7 |
| ('g', '</w>') | 6 |
| ('t', 'h') | 5 |
| ('h', 'e') | 1 |
| ('e', '</w>' | 2 |
| ('a', 'd') | 1 |
| ('d', '</w>') | 1 |
Byte-Pair count
\vdots
\vdots
Word count
| Character | Frequency |
|---|---|
| 'k' | 3 |
| 'n' | 13 |
| 'o' | 9 |
| 'i' | 10 |
| '</w>' | 16 |
| "'" | 1 |
Initial Vocabulary
Merge the most commonly occurring pair : \((i,n) \rightarrow in\)
\vdots
\vdots
| "in" | 7 |
| Word | Frequency |
|---|---|
| 'k n o w i n g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h i n g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h i n g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h i n g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
| Word | Frequency |
|---|---|
| ('k', 'n') | 3 |
| ('n', 'o' | 3 |
| ('o', 'w') | 3 |
| ('w', 'i') | 3 |
| ('i', 'n') | 7 |
| ('n', 'g') | 7 |
| ('g', '</w>') | 6 |
| ('t', 'h') | 5 |
| ('h', 'e') | 1 |
| ('e', '</w>' | 2 |
| ('a', 'd') | 1 |
| ('d', '</w>') | 1 |
Byte-Pair count
\vdots
\vdots
Word count
| Character | Frequency |
|---|---|
| 'k' | 3 |
| 'n' | 13 -7 = 6 |
| 'o' | 9 |
| 'i' | 10-7 = 3 |
| '</w>' | 16 |
| "'" | 1 |
Updated Vocabulary
Merge the most commonly occurring pair
\vdots
\vdots
| "in" | 7 |
Update token count
Added new token
| Word | Frequency |
|---|---|
| 'k n o w in g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h in g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h in g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h in g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
| Word | Frequency |
|---|---|
| ('k', 'n') | 3 |
| ('n', 'o' | 3 |
| ('o', 'w') | 3 |
| ('w', 'i') | 3 |
| ('i', 'n') | 7 |
| ('n', 'g') | 7 |
| ('g', '</w>') | 6 |
| ('t', 'h') | 5 |
| ('h', 'e') | 1 |
| ('e', '</w>' | 2 |
| ('a', 'd') | 1 |
| ('d', '</w>') | 1 |
Byte-Pair count
\vdots
\vdots
Word count
| Character | Frequency |
|---|---|
| 'k' | 3 |
| 'n' | 6 |
| 'o' | 9 |
| 'i' | 3 |
| '</w>' | 16 |
| "'" | 1 |
| 'g': 7 | 7 |
Updated vocabulary
\vdots
\vdots
| "in" | 7 |
Now, treat "in" as a single token and repeat the steps.
| Word | Frequency |
|---|---|
| 'k n o w in g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h in g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h in g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h in g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
| Word | Frequency |
|---|---|
| ('k', 'n') | 3 |
| ('n', 'o' | 3 |
| ('o', 'w') | 3 |
| ('w','in') | 3 |
| ('in', 'g') | 7 |
| ('g', '</w>') | 6 |
| ('t', 'h') | 5 |
| ('h', 'e') | 1 |
| ('e', '</w>' | 2 |
| ('a', 'd') | 1 |
| ('d', '</w>') | 1 |
Byte-Pair count
\vdots
\vdots
Word count
| Character | Frequency |
|---|---|
| 'k' | 3 |
| 'n' | 6 |
| 'o' | 9 |
| 'i' | 3 |
| '</w>' | 16 |
| "'" | 1 |
| 'g': 7 | 7 |
Updated vocabulary
\vdots
\vdots
| "in" | 7 |
| "ing" | 7 |
Therefore, the new byte pairs are (w,in):3,(in,g):7, (h,in):4
Note, at iteration 4, we treat (w,in) as a pair instead of (w,i)
| Word | Frequency |
|---|---|
| 'k n o w in g </w>' | 3 |
| 't h e </w> | 1 |
| 'n a m e </w> | 1 |
| 'o f </w>' | 1 |
| 's o m e t h in g </w> | 2 |
| 'i s </w>' | 1 |
| 'd i f f e r e n t </w>' | 1 |
| 'f r o m </w>' | 1 |
| 's o m e t h in g . </w>' | 1 |
| 'a b o u t </w>' | 1 |
| 'e v e r y t h in g </w>' | 1 |
| "i s n ' t </w> | 1 |
| 'b a d </w>' | 1 |
| Word | Frequency |
|---|---|
| ('k', 'n') | 3 |
| ('n', 'o' | 3 |
| ('o', 'w') | 3 |
| ('w', 'in') | 3 |
| ('h', 'in') | 4 |
| ('in', 'g') | 7 |
| ('g', '</w>') | 6 |
| ('t', 'h') | 5 |
| ('h', 'e') | 1 |
| ('e', '</w>' | 2 |
| ('a', 'd') | 1 |
| ('d', '</w>') | 1 |
Byte-Pair count
\vdots
\vdots
Word count
| Character | Frequency |
|---|---|
| 'k' | 3 |
| 'n' | 6 |
| 'o' | 9 |
| 'i' | 3 |
| '</w>' | 16 |
| "'" | 1 |
| 'g': 7 | 7 |
Updated vocabulary
\vdots
\vdots
| "in" | 7 |
| "ing" | 7 |
Of all these pairs, merge most frequently occurring byte-pairs
which turns out to be "ing"
Now, treat "ing" as a single token and repeat the steps
After 45 merges
| 'k n o w i n g </w>' |
| 't h e </w> |
| 'n a m e </w> |
| 'o f </w>' |
| 's o m e t h i n g </w> |
| 'i s </w>' |
| 'd i f f e r e n t </w>' |
| 'f r o m </w>' |
| 's o m e t h i n g . </w>' |
| 'a b o u t </w>' |
| 'e v e r y t h' |
| "i s n ' t </w> |
| 'b a d </w>' |
The final vocabulary contains initial vocabulary and all the merges (in order). The rare words are broken down into two or more subwords
At test time, the input word is split into a sequence of characters, and the characters are merged into larger known symbols
everything
tokenizer
everyth
ing
The pair ('i','n') is merged first and follwed by the pair ('in','g')
For a larger corpus, we often end up with a vocabulary whose size is smaller than considering individual words as tokens
everything
bad
tokenizer
b
d
bad
a
| Tokens |
|---|
| 'k' |
| 'n' |
| 'o' |
| 'i' |
| '</w>' |
| 'in' |
| 'ing' |
\vdots
The algorithm offers a way to adjust the size of the vocabulary as a function of the number of merges.
\vdots
BPE for non-segmented languages
Languages such as Japanese and Korean are non-segmented
However, BPE requires space-separated words
How do we apply BPE for non-segmented languages then?
In practice, we can use language specific morphology based word segmenters such as Juman++ for Japanese (as shown in the figure on the right)
映画『トランスフォーマー』を楽しく見ました
Input text
Pre-tokenization
Word level Segmenter
Juman++ (or) Mecab
Run BPE
[Eiga, toransufōmā, o, tanoshi,#ku, mi,#mashita][Eiga, toransufōmā, o, tanoshiku, mimashita]However, in the case of multilingual translation, having a language agnostic tokenizer is desirable.
Example:
\(\mathcal{V}=\{a,b,c,\cdots,z,lo,he\}\)
Tokenize the text "hello lol"
[hello],[lol]
search for the byte-pair 'lo', if present merge
Yes. Therefore, Merge
[h e l lo], [lo l]
search for the byte-pair 'he', if present merge
Yes. Therefore, Merge
[he l lo], [lo l]
return the text after merge
he #l #lo, lo #l
Module 1.2 : WordPiece
AI4Bharat, Department of Computer Science and Engineering, IIT Madras
Mitesh M. Khapra
In BPE we merged a pair of tokens which has the highest frequency of occurence.
Take the frequency of occurrence of individual tokens in the pair into account
| Word | Frequency |
|---|---|
| ('k', 'n') | 3 |
| ('n', 'o') | 3 |
| ('o', 'w') | 3 |
| ('w', 'i') | 3 |
| ('i', 'n') | 7 |
| ('n', 'g') | 7 |
| ('g', '.') | 1 |
| ('t', 'h') | 5 |
| ('h', 'e') | 1 |
| ('e', '</w>') | 2 |
| ('a', 'd') | 1 |
\vdots
\vdots
What if there are more pairs that are occurring with the same frequency, for example ('i','n') and ('n','g')?
score=\frac{count(\alpha,\beta)}{count(\alpha)count(\beta)}
Now we can select a pair of tokens where the individual tokens are less frequent in the vocabulary
The WordPiece algorithm uses this score to merge the pairs.
| Word | Frequency |
|---|---|
| 'k n o w i n g' | 3 |
| 't h e ' | 1 |
| 'n a m e ' | 1 |
| 'o f ' | 1 |
| 's o m e t h i n g ' | 2 |
| 'i s ' | 1 |
| 'd i f f e r e n t ' | 1 |
| 'f r o m ' | 1 |
| 's o m e t h i n g. ' | 1 |
| 'a b o u t ' | 1 |
| 'e v e r y t h i n g ' | 1 |
| "i s n ' t ' | 1 |
| 'b a d ' | 1 |
Word count
| Character | Frequency |
|---|---|
| 'k' | 3 |
| '#n' | 13 |
| '#o' | 9 |
| 't' | 16 |
| '#h' | 5 |
| "'" | 1 |
Initial Vocab Size :22
\vdots
\vdots
\vdots
\vdots
knowing
k #n #o #w #i #n #g
Subwords are identified by prefix ## (we use single # for illustration)
Word count
| Word | Frequency |
|---|---|
| 'k n o w i n g' | 3 |
| 't h e ' | 1 |
| 'n a m e ' | 1 |
| 'o f ' | 1 |
| 's o m e t h i n g ' | 2 |
| 'i s ' | 1 |
| 'd i f f e r e n t ' | 1 |
| 'f r o m ' | 1 |
| 's o m e t h i n g. ' | 1 |
| 'a b o u t ' | 1 |
| 'e v e r y t h i n g ' | 1 |
| "i s n ' t ' | 1 |
| 'b a d ' | 1 |
| Word | Frequency |
|---|---|
| ('k', 'n') | 3 |
| ('n', 'o') | 3 |
| ('o', 'w') | 3 |
| ('w', 'i') | 3 |
| ('i', 'n') | 7 |
| ('n', 'g') | 7 |
| ('g', '.') | 1 |
| ('t', 'h') | 5 |
| ('h', 'e') | 1 |
| ('e', '</w>') | 2 |
| ('a', 'd') | 1 |
\vdots
\vdots
ignoring the prefix #
| Freq of 1st element | Freq of 2nd element | score |
|---|---|---|
| 'k':3 | 'n':13 | 0.076 |
| 'n':13 | 'o':9 | 0.02 |
| 'o':9 | 'w':3 | 0.111 |
| 'i':10 | 'n':13 | 0.05 |
| 'n':13 | 'g':7 | 0.076 |
| 't':8 | 'h':5 | 0.125 |
| 'a':3 | 'd':2 | 0.16 |
score=\frac{count(\alpha,\beta)}{count(\alpha)count(\beta)}
Now, merging is based on the score of each byte pair.
Merge the pair with highest score
Small Vocab
Larger Vocab
Medium
Vocab
N \quad Merges
More \quad Merges
We start with a character level vocab
1-112
30K-50K
100K-250K
and keep merging until a desired vocabulary size is reached
Small Vocab
Larger Vocab
Medium
Vocab
More \quad Elimination
N \quad eliminations
We start with word level vocab
1-112
30K-50K
100K-250K
and keep eliminating words until a desired vocabulary size is reached
Well, we can do the reverse as well.
That's what we will see next.
Module 1.3 : SentencePiece
AI4Bharat, Department of Computer Science and Engineering, IIT Madras
Mitesh M. Khapra
\mathbf{x_1}=he,ll,o
\mathbf{x_3}=he,l,lo
\mathbf{x_2}=h,el,lo
\mathbf{x_4}=hell,o
A given word can have numerous subwords.
\(\mathcal{V}\)={h,e,l,l,o,he,el,lo,ll,hell}
however, following the merge rule, BPE outputs
:he,l,lo
On the other hand, if
\(\mathcal{V}\)={h,e,l,l,o,el,he,lo,ll,hell}
then BPE outputs:
h,el,lo
Therefore, we say BPE is greedy and deterministic (we can use BPE-Dropout [Ref] to make it stochastic)
For instance, the word "\(X\)=hello" can be segmented in multiple ways (by BPE) even with the same vocabulary
The probabilistic approach is to find the subword sequence \(\mathbf{x^*} \in \{\mathbf{x_1},\mathbf{x_2},\cdots,\mathbf{x_k}\}\) that maximizes the likelihood of the word \(X\)
The word \(X\) in sentencepiece means a sequence of characters or words (without spaces)
Therefore, it can be applied to languages (like Chinese and Japanese) that do not use any word delimiters in a sentence.
X
All possible subwords of \(X\)
hidden
observed
Let \(\mathbf{x}\) denote a subword sequence of length \(n\).
P(\mathbf{x}) = \prod\limits_{i=1}^{n} P(x_i)
\mathbf{x}^* = \argmax_{\mathbf{x} \in S(X)} P(\mathbf{x})
\sum \limits_{x \in \mathcal{V}} p(x)=1
\mathbf{x}=(x_1, x_2, \dots, x_n)
then the probability of the subword sequence (with unigram LM) is simply
the objective is to find the subword sequence for the input sequence \(X\) (from all possible segmentation candidates of \(S(X)\)) that maximizes the (log) likelihood of the sequence
Recall that the subwords \(p(x_i)\) are hidden (latent) variables.
Then, for all the sequences in the dataset \(D\), we define the likelihood function as
\mathcal{L}= \sum \limits_{s=1}^{|D|}\log(P(X^s))
= \sum \limits_{s=1}^{|D|}\log \Big(\sum \limits_{\mathbf{x} \in S(X^s)} P(\mathbf{x}) \Big)
Therefore, given the vocabulary \(\mathcal{V}\), Expectation-Maximization (EM) algorithm could be used to maximize the likelihood
We can use Viterbi decoding to find \(\mathbf{x}^*\).
| Word | Frequency |
|---|---|
| 'k n o w i n g' | 3 |
| 't h e ' | 1 |
| 'n a m e ' | 1 |
| 'o f ' | 1 |
| 's o m e t h i n g ' | 2 |
| 'i s ' | 1 |
| 'd i f f e r e n t ' | 1 |
| 'f r o m ' | 1 |
| 's o m e t h i n g. ' | 1 |
| 'a b o u t ' | 1 |
| 'e v e r y t h i n g ' | 1 |
| "i s n ' t ' | 1 |
| 'b a d ' | 1 |
Let \(X=\) "knowing" and a few segmentation candidates be \(S(X)=\{`k,now,ing`,`know,ing`,`knowing`\}\)
p(\mathbf{x_1}=k,now,ing)
=p(k)p(now)p(ing)
=\frac{3}{16} \times \frac{3}{16} \times \frac{7}{16}
=\frac{63}{4096}
p(\mathbf{x_2}=know,ing)
=p(know)p(ing)
=\frac{21}{256}=\frac{336}{4096}
p(\mathbf{x_3}=knowing)
=p(knowing)
=\frac{3}{16}=\frac{768}{4096}
Unigram model favours the segmentation with least number of subwords
Given the unigram language model we can calculate the probabilities of the segments as follows
\mathbf{x}^* = \argmax_{\mathbf{x} \in S(X)} P(\mathbf{x})=\mathbf{x_3}
In practice, we use Viterbi decoding to find \(\mathbf{x}^*\) instead of enumerating all possible segments
-
Construct a reasonably large seed vocabulary using BPE or Extended Suffix Array algorithm.
-
E-Step:
Estimate the probability for every token in the given vocabulary using frequency counts in the training corpus
-
M-Step:
Use Viterbi algorithm to segment the corpus and return optimal segments that maximizes the (log) likelihood.
-
Compute the likelihood for each new subword from optimal segments
-
Shrink the vocabulary size by removing top \(x\%\) of subwords that have the smallest likelihood.
-
Repeat step 2 to 5 until desired vocabulary size is reached
Algorithm
Set the desired vocabulary size
Let us consider segmenting the word "whereby" using Viterbi decoding
k
a
no
b
e
d
f
now
bow
bo
in
om
ro
ry
ad
ng
out
eve
win
some
bad
owi
ing
hing
thing
g
z
er
\mathcal{V}
| Token | log(p(x)) |
|---|---|
| b | -4.7 |
| e | -2.7 |
| h | -3.34 |
| r | -3.36 |
| w | -4.29 |
| wh | -5.99 |
| er | -5.34 |
| where | -8.21 |
| by | -7.34 |
| he | -6.02 |
| ere | -6.83 |
| here | -7.84 |
| her | -7.38 |
| re | -6.13 |
w\\-4.29
t=1
whereby
Forward algorithm
Iterate over every position in the given word
output the segment which has the highest likelihood
w
| Token | log(p(x)) |
|---|---|
| b | -4.7 |
| e | -2.7 |
| h | -3.34 |
| r | -3.36 |
| w | -4.29 |
| wh | -5.99 |
| er | -5.34 |
| where | -8.21 |
| by | -7.34 |
| he | -6.02 |
| ere | -6.83 |
| here | -7.84 |
| her | -7.38 |
| re | -6.13 |
h
wh
-7.63
-5.99
whereby
w
(w,h)
At this position, the posible segmentations of the slice "wh" are (w,h) and (wh)
Compute the log-likelihood for both and output the best one.
| Token | log(p(x)) |
|---|---|
| b | -4.7 |
| e | -2.7 |
| h | -3.34 |
| r | -3.36 |
| w | -4.29 |
| wh | -5.99 |
| er | -5.34 |
| where | -8.21 |
| by | -7.34 |
| he | -6.02 |
| ere | -6.83 |
| here | -7.84 |
| her | -7.38 |
| re | -6.13 |
whereby
h
wh
-7.63
-5.99
e
-10.33
he
-10.31
e
-8.69
We do not need to compute the likelihood of (w,h,e) as we already ruled out (w,h) in favor of (wh). We display it for completeness
whe
-\infty
Of these, (wh,e) is the best segmentation that maximizes the likelihood.
w
| Token | log(p(x)) |
|---|---|
| b | -4.7 |
| e | -2.7 |
| h | -3.34 |
| r | -3.36 |
| w | -4.29 |
| wh | -5.99 |
| er | -5.34 |
| where | -8.21 |
| by | -7.34 |
| he | -6.02 |
| ere | -6.83 |
| here | -7.84 |
| her | -7.38 |
| re | -6.13 |
whereby
wh
-5.99
he
-10.31
e
-8.69
whe
-\infty
\times
\times
her
-11.67
er
-11.33
r
-12.05
wher
-\infty
h
w
\times
-7.63
| Token | log(p(x)) |
|---|---|
| b | -4.7 |
| e | -2.7 |
| h | -3.34 |
| r | -3.36 |
| w | -4.29 |
| wh | -5.99 |
| er | -5.34 |
| where | -8.21 |
| by | -7.34 |
| he | -6.02 |
| ere | -6.83 |
| here | -7.84 |
| her | -7.38 |
| re | -6.13 |
whereby
wh
-5.99
he
-10.31
e
-8.69
whe
-\infty
\times
\times
her
-11.67
er
-11.33
r
-12.05
wher
\times
-\infty
\times
where
-8.21
h
w
\times
here
-10.54
\times
e
-14.03
ere
-12.82
\times
-7.63
| Token | log(p(x)) |
|---|---|
| b | -4.7 |
| e | -2.7 |
| h | -3.34 |
| r | -3.36 |
| w | -4.29 |
| wh | -5.99 |
| er | -5.34 |
| where | -8.21 |
| by | -7.34 |
| he | -6.02 |
| ere | -6.83 |
| here | -7.84 |
| her | -7.38 |
| re | -6.13 |
whereby
wh
-5.99
he
-10.31
e
-8.69
whe
-\infty
\times
\times
her
-11.67
er
-11.33
r
-12.05
wher
\times
-\infty
\times
where
-8.21
h
w
\times
here
-10.54
\times
e
-14.03
ere
-12.82
\times
-7.63
whereb
-\infty
b
-12.91
| Token | log(p(x)) |
|---|---|
| b | -4.7 |
| e | -2.7 |
| h | -3.34 |
| r | -3.36 |
| w | -4.29 |
| wh | -5.99 |
| er | -5.34 |
| where | -8.21 |
| by | -7.34 |
| he | -6.02 |
| ere | -6.83 |
| here | -7.84 |
| her | -7.38 |
| re | -6.13 |
whereby
wh
-5.99
he
-10.31
e
-8.69
whe
-\infty
\times
\times
her
-11.67
er
-11.33
r
-12.05
wher
\times
-\infty
\times
where
-8.21
h
w
\times
here
-10.54
\times
e
-14.03
ere
-12.82
\times
-7.63
whereb
-\infty
b
-12.91
by
-15.51
\times
\times
\times
| Token | log(p(x)) |
|---|---|
| b | -4.7 |
| e | -2.7 |
| h | -3.34 |
| r | -3.36 |
| w | -4.29 |
| wh | -5.99 |
| er | -5.34 |
| where | -8.21 |
| by | -7.34 |
| he | -6.02 |
| ere | -6.83 |
| here | -7.84 |
| her | -7.38 |
| re | -6.13 |
Backtrack
whereby
wh
-5.99
he
-10.31
e
-8.69
whe
-\infty
\times
\times
her
-11.67
er
-11.33
r
-12.05
wher
\times
-\infty
\times
where
-8.21
h
w
\times
here
-10.54
\times
e
-14.03
ere
-12.82
\times
-7.63
whereb
-\infty
b
-12.91
by
-15.51
The best segmentation of the word "whereby" that maximizes the likelihood is "where,by"
\times
\times
\times
We can follow the same procedure for languages that do not use any word delimiters in a sentence.
Module 2 : HF Tokenizers
AI4Bharat, Department of Data Science and Artificial Intelligence, IIT Madras
Mitesh M. Khapra
Recall the general Pre-processing pipeline
Hmm.., I know I Don't know
Input text
hmm.., i know i don't know
Normalization
Pre-tokenization
[hmm.., i, know, i , don't,know]
Tokenization using learned vocab
HF tokenizers module provides a class that encapsulates all of these components
from tokenizers import Tokenizer[hmm.., i, know, i, do, #n't,know]
Post Processing (add model specific tokens)
pre-tokenizer
normalizer
Tokenizer
Algorithm (model)
Post Processor
[<go>,hmm.., i, know, i, do, #n't,know,<end>]
HF tokenizers module provides a class that encapsulates all of these compoents
from tokenizers import Tokenizerpre-tokenizer
normalizer
Tokenizer
Algorithm (model)
Post Processor
We can customize each step of the tokenizer pipeline
WhiteSpace, Regex, BERTlike
BPE,WordPiece..
LowerCase, StripAccents
Choices
Insert model specific tokens
via the setter and getter properties of the class (just like a plug-in)
Property (getter and setter,del)
-
model
-
normalizer
-
pre_tokenizer
-
post_processor
-
padding (no setter)
-
truncation (no setter)
-
decoder
tokenizer = Tokenizer(BPE())
#doesn't matter order in which the properties are set
tokenizer.pre_tokenizer = Whitespace()
tokenizer.normalizer = Lowercase()pre-tokenizer
normalizer
Tokenizer
Algorithm (model)
Post Processor
WhiteSpace
BPE
LowerCase
[CLS],[SEP]
tokenizer = Tokenizer(BPE())
#doesn't matter order in which the properties are set
tokenizer.pre_tokenizer = Whitespace()
tokenizer.normalizer = Lowercase()Learning the vocabualty
Provides set of methods for training (learn the vocabulary), encoding input and decoding predictions and so on
-
add_special_tokens(str,AddedToken)
-
no token_ids are assigned
-
-
add_tokens()
-
enable_padding(), enable_truncation()
-
encode(seq,pair,is_pretokenized), encode_batch()
-
decode(),decode_batch()
-
from_file(.json) # serialized local json file
-
from_pretrained(.json) # from hub
-
get_vocab(), get_vocab_size()
-
id_to_token(), token_to_id()
-
post_process()
-
train(files), train_from_iterator(dataset)
Tokenizer
# Core Class
class tokenizers.Tokenizer.train_from_iterator(dataset, trainer)
Object
We do not need to call each of these methods sequentially to build a tokenizer
After setting Normalizer and Pre-Tokenizer, we just need to call the train methods to build the vocabulary
List of strings (text)
(vocab_size, special_tokens,prefix,..)
Once the training is complete, we can call methods such as encode for encoding the input string
What should be the output if we call encode_batch method?
Encoding Class
Tokenizer
Object
Assume that the tokenizer has been trained (i.e., learned the vocabulary)
['This is great','tell me a joke']
{input_ids, attention_mask, type_ids, ..}
The output is a dictionary that contains not only input_ids but also optional outputs like attention_mask, type_ids (which we will learn about in the next lecture)
We can customize the output behaviour by passing the instance of Encoding object to the post_process() methods of Tokenizer (it is used internally, we can just set the desired formats in the optional parameters like "pair" in encode())
encoding = Encoding()
tokenizer.post_process(encoding,pair=True)Customization
It is possible to customize each component as desired. However, we will not go into details in this course.
The takeaway is that we can build and train a tokenizer on any dataset (regardless of size) in 6 to 8 lines of code!
DLP-Lecture-2
By Arun Prakash
