Linear Regression - Kernel Regression
Arun Prakash A
Supervised: Samples \(X\) and Label \(y\)
Regression
Classification
Binary
Multiclass
Simple/Multiple
Multivariate
Multilabel
X \in \mathbb{R}^{d \times n}
Dataset : \(\{X,y\}\)
y \in \mathbb{R}^{n}
\(n\) samples, \(d\) features
\(y\) target/label
A single training example is a pair \(\{x_i,y_i\}\)
i \rightarrow
j \\
\downarrow
features
samples
Supervised Learning: Regression
X \in \mathbb{R}^{n \times d}
Dataset : \(\{X,y\}\)
y \in \mathbb{R}^{n}
Example: \(d=1\)
We can either treat the feature "price" or the feature " living area in square feet" as a target variable \(y\)
True or False?
\(n\) samples, \(d\) features
\(y\) target/label
A single training example is a pair \(\{x_i,y_i\}\)
Example: \(d=1\)
We can either treat the feature "price" or the feature " living area in square feet" as a target variable \(y\)
True or False?
Regression is always linear.
True or False?
Assume a Linear relation
y=x^Tw
L(w)=\frac{1}{2}\sum \limits_{i=1}^n(x_i^Tw-y_i)^2
x_i,w \in \mathbb{R}^{d \times 1}
\frac{\partial L}{\partial w_j}=\frac{1}{2}\sum \limits_{i=1}^n(x_i^Tw-y_i)^2
=\frac{1}{2}\sum \limits_{i=1}^n 2(x_i^Tw-y_i)x_{ji}
= [(x_1^Tw-y_1)x_{j1}+(x_2^Tw-y_2)x_{j2}+\cdots+(x_n^Tw-y_n)x_{jn}]
Let's write it compactly!
\begin{bmatrix}
x_1^Tw-y_1 \\
x_2^Tw-y_2\\
\vdots \\
x_n^Tw-y_n
\end{bmatrix}
\begin{bmatrix}
x_{j1}&x_{j2}&\cdots & x_{jn}
\end{bmatrix}
\frac{\partial L}{\partial w_j}=
\begin{bmatrix}
x_1^Tw-y_1 \\
x_2^Tw-y_2\\
\vdots \\
x_n^Tw-y_n
\end{bmatrix}
\begin{bmatrix}
x_{j1}&x_{j2}&\cdots & x_{jn}
\end{bmatrix}
\frac{\partial L}{\partial w_j}=
j=1,2,\cdots,d
\begin{bmatrix}
x_{11}&x_{12}&\cdots & x_{1n} \\
x_{21}&x_{22}&\cdots & x_{2n}\\
\vdots \\
x_{d1} &x_{d2} & \cdots & x_{dn}
\end{bmatrix}
\begin{bmatrix}
x_1^Tw-y_1 \\
x_2^Tw-y_2\\
\vdots \\
x_n^Tw-y_n
\end{bmatrix}
\begin{bmatrix}
\frac{\partial L}{\partial w_1} \\
\frac{\partial L}{\partial w_2}\\
\vdots \\
\frac{\partial L}{\partial w_d}
\end{bmatrix}=
\nabla_w L = \quad \quad X \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad(X^Tw-y)
\nabla_w L = X X^Tw-Xy
\nabla_w L = X X^Tw-Xy
w^*=(XX^T)^{-1}Xy
Set the gradient to zero to find \(w^*\)
Use pseudo inverse if inverse doesn't exist ( because pseudo inverse matrix satisfies all the properties that an inverse matrix satisfy )
h_x=X^Tw^*=X^T(XX^T)^{-1}Xy
\nabla_w^2 L = X X^T
Hessian. If \(XX^T\) is PSD, the solution is unique
Info Byte
That is, the columns of \(X\) has to be linearly independent
X^T(XX^T)^{-1}X
h_x=X^Tw^*=
y
X^T(XX^T)^{-1}X
is called the projection matrix
From Deterministic to Random
y=x^Tw
We are not sure whether the observed \(d\) features are sufficient to explain the observed \(y\) .
We might have missed some features (correlated or uncorrelated) that could potentially relate to \(y\)
We could model this as a random variable \(\epsilon\) (or noise), that could explain the deviation in the prediction.
y=x^Tw+\epsilon
\epsilon \sim \mathcal{N}(0,\sigma^2)
\(\epsilon\) could follow any distribution, generally assumed to be normal if not specified otherwise
\circ
\circ
\circ
\epsilon
\epsilon
\epsilon
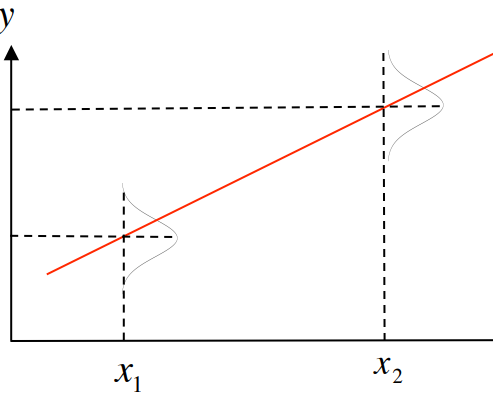
This gives a fixed value for \(y\) for given \(x\) .
However, we can see that prediction deviates from the actual values. (there could be more than one value for \(y\) for given \(x\))
Now, the prediction is the expectation of \(y,E[y|x]\) (the value of \(y\) on an average for the given \(x\))
x
y
p(\epsilon_i)=\frac{1}{\sqrt{2 \pi}\sigma}exp(\frac{-(\epsilon_i^2)}{2\sigma^2})
This gives us
p(y_i|x_i;w)=\frac{1}{\sqrt{2 \pi}\sigma}exp(\frac{-(y_i-x_i^Tw)^2}{2\sigma^2})
mean
Likelihood of \(y\) given \(x\)
p(y|X;w)=\prod \limits_{i=1}^n \frac{1}{\sqrt{2 \pi}\sigma}exp(\frac{-(y_i-x_i^Tw)^2}{2\sigma^2})
Maximize log-likelihood
p(y|X;w)=\prod \limits_{i=1}^n \frac{1}{\sqrt{2 \pi}\sigma}exp(\frac{-(y_i-x_i^Tw)^2}{2\sigma^2})
\log(p(y|X;w))=\log\Big(\prod \limits_{i=1}^n \frac{1}{\sqrt{2 \pi}\sigma}exp(\frac{-(y_i-x_i^Tw)^2}{2\sigma^2})\Big)
=\log\Big(\prod \limits_{i=1}^n \frac{1}{\sqrt{2 \pi}\sigma}exp(\frac{-(y_i-x_i^Tw)^2}{2\sigma^2})\Big)
=\sum\limits_{i=1}^n \log\Big(\frac{1}{\sqrt{2 \pi}\sigma}exp(\frac{-(y_i-x_i^Tw)^2}{2\sigma^2})\Big)
=n \log \frac{1}{\sqrt{2 \pi}\sigma}-\sum\limits_{i=1}^n \frac{(y_i-x_i^Tw)^2}{2\sigma^2}
=n \log \frac{1}{\sqrt{2 \pi}\sigma}-\frac{1}{2\sigma^2}\sum\limits_{i=1}^n (y_i-x_i^Tw)^2
Maximizing the log-likelihood is equivalent to minimizing the sum square error.
Computational complexity
w^*=(XX^T)^{-1}Xy
Complexity: \(O(d^3)\), requires all samples
Use an iterative algorithm: Gradient Descent
\nabla_{w_t} = 2(X X^Tw_t-Xy)
w_{t+1}=w_t-\eta_t \nabla_{w_t}
Initialize \(w\) randomly and compute the gradient
Update \(w\)
Repeat until the loss (or gradient) becomes zero.
Go with stochastic gradient descent if we do not have enough compute.
Non-Linear Regression (Kernel Regression)
y=w_0+w_1x
y=w_0+w_1x+w_2x^2
y=w_0+w_1x+w_2x^2+\cdots
Fit datapoints globally
X \to \Phi(X)
\hat{y}=X^Tw
X^T \in \mathbb{R}^{n \times d}
w \in \mathbb{R}^{d \times 1}
Linear regression
Kernel Regression
w^*=(XX^T)^{-1}Xy
\hat{y}=X\alpha
w^*=X\alpha^*
w.k.t
Computing \(XX^T\) is costly for \(d>>n\)
w^*=X\alpha^*=(XX^T)^{-1}Xy
X\alpha^*=(XX^T)^{-1}Xy
Manipulating it further
\alpha^*=K^{-1}y
y_{test}=\sum \limits_{i=1}^n \alpha_iK(x_i,x_{test})
y_{test}=\Big(\sum \limits_{i=1}^n \alpha_i \phi(x_i)\Big)^T\phi(x_{test})
during testing
\hat{y}=X\alpha
w^*=X\alpha^*
w.k.t
Kernel maps the data points to infinite dimension, then it requires infinite number of parameters in the transformed domain. So, does it always overfit the training data points.?
No. It overfits when \(K\) has a full rank (therefore, inverse exists). In practice, it rarely occurs when we have number of samples equals to the number of features
Summary of Important concepts
Supervised: Samples \(X\) and Label \(y\)
Regression
Classification
Binary
Multiclass
Simple/Multiple
Multivariate
Multilabel
X \in \mathbb{R}^{d \times n}
Data : \(\{X,y\}\)
y \in \mathbb{R}^{n}
i \rightarrow
j \\
\downarrow
features
samples
Linear Regression: Solving via Normal Equations
Model : Linear
\hat{y}=x_i^Tw
Loss : Squared Error Loss
L(w)=\sum \limits_{i=1}^n(x_i^Tw-y_i)^2
\(w=w^*\) that minimizes the loss
w^*=(XX^T)^{-1}Xy
X^T(XX^T)^{-1}X
h_x=X^Tw^*=
y
X^T(XX^T)^{-1}X
is called the projection matrix
From Deterministic to Random
\hat{y}=x^Tw
\circ
\circ
\circ
\epsilon
\epsilon
\epsilon
x
y
\hat{y}=x^Tw+\epsilon
We could model this as a random variable \(\epsilon\) (or noise), that could explain the deviation in the prediction.
\epsilon \sim \mathcal{N}(0,\sigma^2)
p(\epsilon_i)=\frac{1}{\sqrt{2 \pi}\sigma}exp(\frac{-(\epsilon_i^2)}{2\sigma^2})
p(y_i|x_i;w)=\frac{1}{\sqrt{2 \pi}\sigma}exp(\frac{-(y_i-x_i^Tw)^2}{2\sigma^2})
mean
Likelihood of \(y\) given \(x\)
p(y|X;w)=\prod \limits_{i=1}^n \frac{1}{\sqrt{2 \pi}\sigma}exp(\frac{-(y_i-x_i^Tw)^2}{2\sigma^2})
Maximize log-likelihood
=n \log \frac{1}{\sqrt{2 \pi}\sigma}-\frac{1}{2\sigma^2}\sum\limits_{i=1}^n (y_i-x_i^Tw)^2
Maximizing the log-likelihood is equivalent to minimizing the sum square error.
Computational complexity
w^*=(XX^T)^{-1}Xy
Complexity: \(O(d^3)\), requires all samples
Use an iterative algorithm: Gradient Descent
\nabla_{w_t} = 2(X X^Tw_t-Xy)
w_{t+1}=w_t-\eta_t \nabla_{w_t}
Initialize \(w\) randomly and compute the gradient
Update \(w\)
Stop the iteration based on some criteria (such as number of iterations, loss_threshold..)
Go with stochastic gradient descent if we do not have enough compute.
\hat{y}=X^Tw
X^T \in \mathbb{R}^{n \times d}
w \in \mathbb{R}^{d \times 1}
Linear regression
Kernel Regression
w^*=(XX^T)^{-1}Xy
\hat{y}=X\alpha
w^*=X\alpha^*
w.k.t
Computing \(XX^T\) is costly for \(d>>n\)
w^*=X\alpha^*=(XX^T)^{-1}Xy
X\alpha^*=(XX^T)^{-1}Xy
Manipulating it further
\alpha^*=K^{-1}y
y_{test}=\sum \limits_{i=1}^n \alpha_iK(x_i,x_{test})
during testing
Linear Regression - Kernel Regression - ProbabilisticView
By Arun Prakash
Linear Regression - Kernel Regression - ProbabilisticView
MLT - Week5 Session slides
