Machine Learning Foundations
Tutorial - Week5
Arun Prakash A
I = \sum\limits_{i=1}^k \sigma_i u_i v_i^T
I = U \Sigma V^T
Our Mind
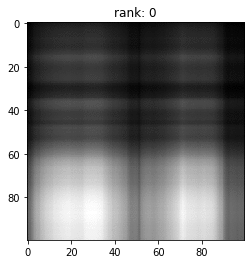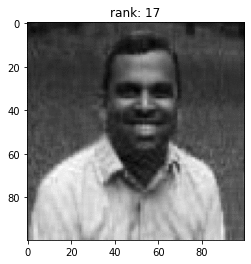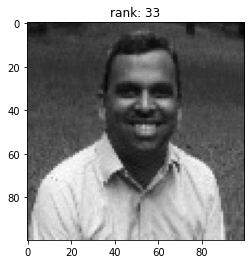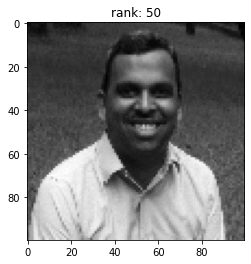
Let's play a game
272
268
\Sigma
U
V^T
268
=
268
268
272
272
272
Image
- I am going to show you a sequence of images, one after another, that contains something.
- Task : Recognise the "thing" in the images. (Note down the sequence number)
- Let's go
My bad: Add +1 to the rank
What do you perceive?
What do you perceive?
What do you perceive?
What do you perceive?
What do you perceive?
What do you perceive?
What do you perceive?
What do you perceive?
What do you perceive?
What do you perceive?
Recognise the man in the picture
Recognise the man in the picture
Recognise the man in the picture
Recognise the man in the picture
Recognise the man in the picture
Recognise the man in the picture
Rank (k =50) Approximation
Of course, we lost some resolution (details)!
But not the gross information!
Image compression
272
268
\Sigma
U
V^T
268
=
268
268
272
272
272
0
0
I = \sum\limits_{i=1}^k \sigma_i u_i v_i^T
=15
\sigma_i = 0 , i>15
272
268
Number of elements to be stored:
268*272 = 72,896
272
Original Image : (Without Compression)
Approx. Image :( or Compressed)
- For \(U\) : 268*15 = 4020
- For \(\Sigma\): \(k\) =15
- For \( V^T\) : 15*272 = 4080
- Total = 8115
- ~= 9 times reduction in required memory for storage
Well, but, hmm..How does it work?
The image is a linear combination of
\sigma_1 = 14.7
\sigma_2 = 5.22
\sigma_3= 3.31
\sigma_i= 0, i>3
It is zero by deafult!
Removes redundancy!
Tutorial - Week5
Arun Prakash A
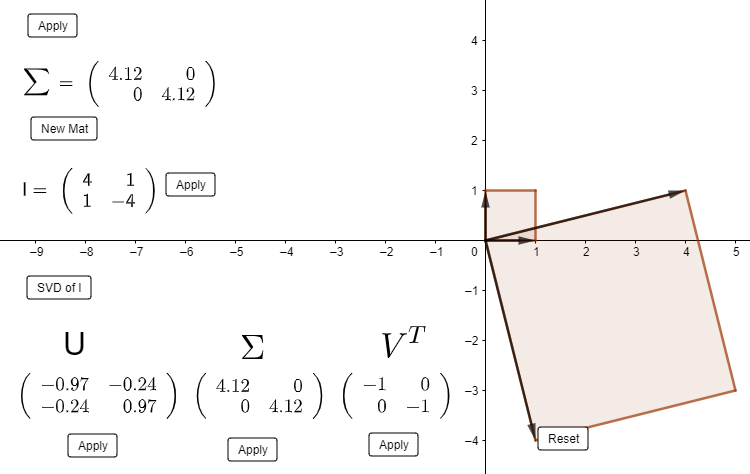
Geometric Interpretation of SVD
SVD
I = U \Sigma V^T
Diagonal Matrix
- What happens if diagonal matrices act on a set of vectors in the canonical (standard) basis?
- Let us see it in \(\mathbb{R}^2\) with help of Geogebra applet :-)
Diagonal Matrices
Diagonal matrices preserves the direction of orthogonal vectors!
Why?
Similar Matrices
Geometry of SVD
Geometry of SVD
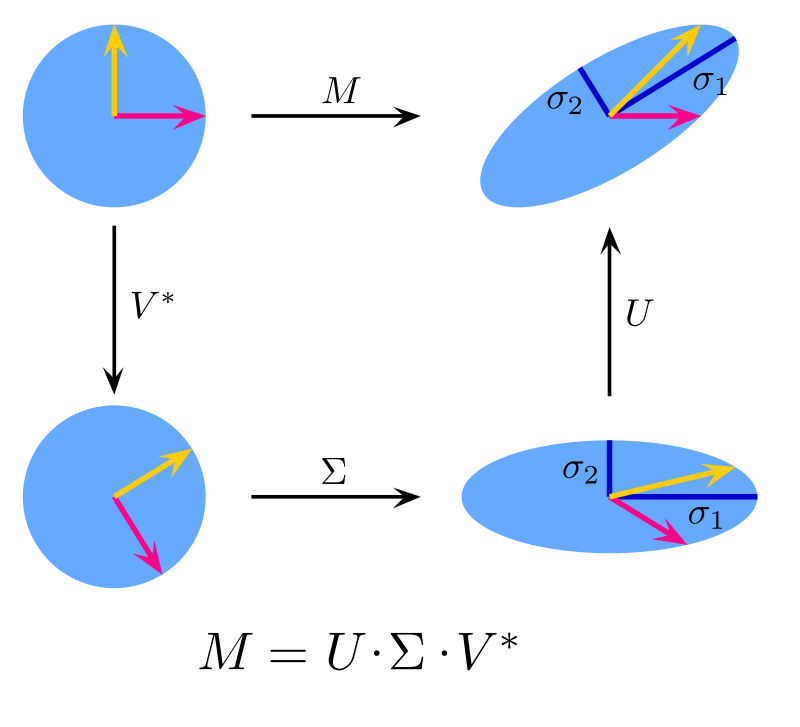
A quick summary:
- \(V^T\) Rotates disk D and basis \(e_1,e_2\)
- \(\Sigma\) scales the rotated disk D and \(\sigma_1,\sigma_2\) are semi-major and semi-minor axis of an ellipse (hyper-ellipse)
- \(U\) rotates the ellipse.
Source: Wikipedia
I = \sum\limits_{i=1}^k \sigma_i u_i v_i^T
I = U \Sigma V^T
Tutorial - Week5
Arun Prakash A
Some questions to think and solve
High Dimensional Visualization
Geoffrey Hinton
"To deal with hyper-planes in a 14-dimensional space, visualize a 3-D space and say 'fourteen' to yourself very loudly. Everyone does it.
1. Is it possible to visualize complex vectors \(x_i \in \mathbb{C}^2\)geometrically as we do for real vectors ?. Pause the video and think about it.
We need 4 dimensions to visualize a vector from \(\mathbb{C}^2\)
x_1
x_2
x = \begin{bmatrix} 1& \\ 1 \end{bmatrix}
Re
i
x = \begin{bmatrix} 1+i & \\ ? \end{bmatrix}
Do complex matrices find any real world applications?
Is that just an abstract mathematical stuff?
\begin{bmatrix}
1 & 1 & 1 & 1 \\
1 & -i & -1 & i \\
1 & -1 & 1 & -1 \\
1 & i & -1 & i \\
\end{bmatrix}
Discrete Fourier Transform (DFT)
Countless Applications in signal processing, Digital communication, Speech processing ...
2.Compute the inner product between two vectors \(x= \begin{bmatrix}3-2i \\-2+i\\-4 - 3i \\ \end{bmatrix} \) and \(y=\begin{bmatrix}-2+4i\\5-i\\-2i\\ \end{bmatrix}\) and verify whether they are commutative (i.e. \(x \cdot y = y \cdot x\))
\( (3+2i) \times (-2+4i)\)
\( (-2-i) \times (5-i)\)
\( (-4+3i) \times (-2i)\)
= \( -14+8i\)
= \( -11-3i\)
= \( 6+8i\)
\( -19+13i\)
\( x \cdot y = x^*y=\bar{x}^Ty\)
\( y\cdot x = y^*x=\bar{y}^Tx\)
2.Compute the inner product between two vectors \(x=[3-2i,-2+i,-4 - 3i]^T\) and \(y=[-2+4i,5-i,-2i]^T\) and verify whether they are commutative (i.e. \(x \cdot y = y \cdot x\))
\( (3-2i) \times (-2-4i)\)
\( (-2+i) \times (5+i)\)
\( (-4-3i) \times (2i)\)
= \( -14-8i\)
= \( -11+3i\)
= \( 6-8i\)
\( -19-13i\)
\( y\cdot x = y^*x=\bar{y}^Tx\)
\(\overline{x \cdot y} \)
\( y\cdot x = y^*x=\bar{y}^Tx\)
\(x \cdot y \neq y \cdot x\)
Is it always true?
3. Prove that \(x \cdot y = \overline{y \cdot x}\) where \( x \in \mathbb{C}^n\) and \( y \in \mathbb{C}^n\)
\(\overline{y \cdot x} = \overline{\bar{y}x} \)
\( = \overline{\bar{y_1}x_1}+\overline{\bar{y_2}x_2} + \cdots +\overline{\bar{y_n}x_n} \)
\( =y_1\bar{x_1}+y_2\bar{x_2}+\cdots+y_n\bar{x_n} \)
\( =\bar{x_1}y_1+\bar{x_2}y_2+\cdots+\bar{x_n}y_n \)
\( = x \cdot y\)
4. Can we use inner product to compute (cosine) angle between two complex vectors, like we do for real vectors?
No!. Not Always
\( \frac{x \cdot y}{||x|| \ ||y||} \)
Let us reason why?
But some authors prefers
\( \frac{Re(x \cdot y)}{||x|| \ ||y||} \)
More details on it : Angles in complex vector space
5. Consider the matrix \(A = \begin{bmatrix}2& 3-3i \\ 3+3i & 5 \\ \end{bmatrix} \). Find the complex eigenvector for the eigenvalue \(\lambda=8\)
R_2 = R_2+\frac{1}{2}(1+i)R_1
N[A-\lambda I] = \begin{bmatrix}-6& 3-3i \\ 3+3i & -3 \\ \end{bmatrix}
= \begin{bmatrix}-6& 3-3i \\ 0 & 0 \\ \end{bmatrix}
\begin{bmatrix}-6& 3-3i \\ 0 & 0 \\ \end{bmatrix}\begin{bmatrix}x_1 \\x_2 \\ \end{bmatrix} = \begin{bmatrix} 0 \\0 \\ \end{bmatrix}
-6x_1+(3-3i)x_2=0
-2x_1+(1-1i)x_2=0
2x_1=(1-1i)x_2
x_1 = 1
x_2 = \frac{2}{1-1i}
x_2 = \frac{2}{1-1i} = \frac{2}{1-1i} \frac{1+1i}{1+1i}
x_2 = 1+1i
\therefore x =\begin{bmatrix}1 \\ 1+1i \\ \end{bmatrix}
6. Let \(U = \begin{bmatrix} cos(t)& -sin(t) \\ sin(t) & cos(t) \end{bmatrix}\), show that the matrix \(U\) is unitary.
U = \begin{bmatrix} cos(t)& -sin(t) \\ sin(t) & cos(t) \end{bmatrix}
U^T= \begin{bmatrix} cos(t)& sin(t) \\ -sin(t) & cos(t) \end{bmatrix}
U*U^T= \begin{bmatrix} cos^2(t)+sin^2(t)& cos(t)sin(t) -sin(t)cos(t)\\ sin(t)cos(t)-cos(t)sin(t) & sin^2(t)+cos^2(t) \end{bmatrix}
U*U^T= \begin{bmatrix} 1& 0\\0 & 1 \end{bmatrix} = I
7. We know that \(U = \begin{bmatrix} cos(t)& -sin(t) \\ sin(t) & cos(t) \end{bmatrix}\),is unitary.Let us take a vector \(x \in R^2\) and see what happens when it get transformed by the \(U\).
MLF_Tutorial_5
By Arun Prakash
