Deep Learning Practice - NLP

Language Modelling, GPT, Pretraining using

HF Transformers

Mitesh M. Khapra

AI4Bharat, Department of Computer Science and Engineering, IIT Madras

 Dataset

So far

import datasets
import transformers
import evalaute

We have learned how to load any dataset from the HF hub, access samples, modify them and save them back using HF datasets module.

We learned how to load any dataset from the HF hub, access  and modify samples, and save them to disk using the HF datasets module.

So far

 Dataset

Encode Text

Initialize  

Model

Decode Predictions

Tokenizer

import datasets
import tokenizers
tokenizer.encode()
tokenizer.decode()

Next, we learned how to train a tokenizer that encodes input text according to the model-specific template and decodes the model's predictions

In this week

 Dataset

Encode Text

Initialize  

Model

Train the model

Decode Predictions

Tokenizer

import datasets
import tokenizers
tokenizer.encode()
tokenizer.decode()
import transformers

we will learn how to train transformer based models using the HF transformers module. 

10 GB
5GB
21GB
40GB
1 GB
100 GB
1000 GB

BookCorpus

Wikipedia

OpenWebText

110GB

RealNews

800GB

C4, The Pile

1600GB

ROOTS

The size of datasets has kept growing

Over the Years

Fruit Fly

Honey Bee

Mouse

Cat

Brain

>10^6
10^9
10^{12}
10^{13}
10^{15}

#  Synapses
400M

Transformer

1.5B

GPT-2

10B

Megatron LM

175B

GPT-3

Here is the Evolution tree 

We can group the transformer based models into three categories

Encoder-only models (BERT and its variants) dominated the field for about two years 

Decoder-only models (GPT) soon emerged for the task of Language modeling

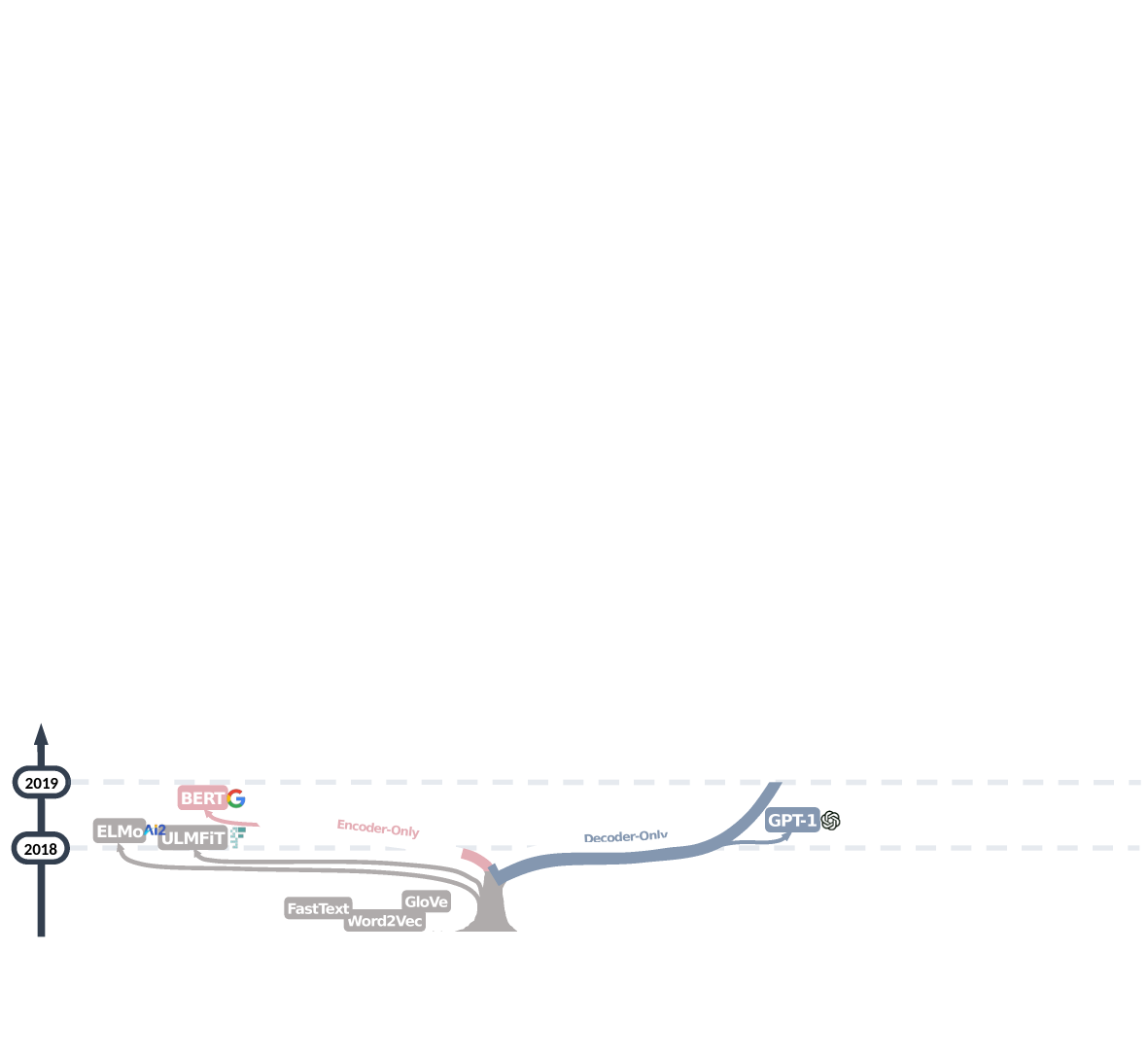
Encoder-only models (BERT and its variants) dominated the field for about two years 

GPT-2 and T5 advocated for decoder only models and encoder-decoder models, respectively.

Model

 Dataset

  • Scale the model or dataset or both?

  • What is the proportion of scaling?

The tree has grown bigger

The tree has grown bigger and bigger 

The tree has grown bigger and bigger in a short span of time

Even if we select only the decoder branch in the evaluation tree

there would still be  dozens of models

However, all of these LLMs go through a phase called pretraining.

Let’s try to understand this using the GPT (Generative Pretrained Transformer) model.

In the DL course, we learned about the components of the transformer architecture in the context of machine translation.

At a higher level of abstraction, we can view it as a black box that takes an input and generates an output.

Transformer

Text in source language

Translated text in target language

In the DL course, we learned about the components of the transformer architecture in the context of machine translation.

Transformer

Transformer

Transformer

Input text

Predict the class/sentiment

Input text

Summarize

Question

Answer

Input text

What if we want to use the transformer architecture for other NLP tasks?

We need to train a separate model for each task using a dataset specific to the task

In the DL course, we learned about the components of the transformer architecture in the context of machine translation.

Transformer

Transformer

Transformer

Input text

Predict the class/sentiment

Input text

Summarize

Question

Answer

Input text

What if we want to use the transformer architecture for other NLP tasks?

We need to train a separate model for each task using dataset specific to the task

If we train the architecture from scratch (that is, by randomly initializing the parameters) for each task, it takes a long time for convergence

Often, we may not have enough labelled samples for many NLP  tasks

Moreover, preparing labelled data is laborious and costly

On the other hand,

we have a large amount of unlabelled text easily available on the internet 

Transformer

Transformer

Transformer

Input text

Predict the class/sentiment

Input text

Summarize

Question

Answer

Input text

Can we make use of such unlabelled data to train a model?

Module 3.1 : Language Modelling

Mitesh M. Khapra

AI4Bharat, Department of Computer Science and Engineering, IIT Madras

Motivation

" Wow, India has now reached the moon"

Is this sentence expressing a positive or a negative sentiment?

An excerpt from business today "What sets this mission apart is the pivotal role of artificial intelligence (AI) in guiding the spacecraft during its critical descent to the moon's surface."

Did the lander use AI for soft landing on the moon?

Assume that we ask questions to a lay person based on a statement or some excerpt

He likes to stay

He likes to stray

He likes to sway

Are these meaningful sentences?

The person will most likely answer all the questions, even though he/she may not be explicitly trained on any of these tasks. How?

We develop a strong understanding of  language through various language based interactions( listening/reading)  over our life time without any explicit supervision

Can a model develop basic understanding of language by getting exposure to a large amount of raw text? [pre-training]

More importantly, after getting exposed to such raw data can it learn to perform well on downstream tasks with minimum supervision? [Supervised Fine-tuning]

Idea

With this representation a linear model classifies reviews with 91.8% accuracy beating the SOTA (Ref)

...matches the performance of previous supervised systems using 30-100x fewer labeled examples (Ref)

Language Modeling

(Pre-training)

Raw text

Downstream tasks

(Fine-tuning)

(Samples and labels)

Language modelling

 Let \(\mathcal{V}\) be a vocabulary of  language (i.e., collection of all unique words in the language)

For example, if \(\mathcal{V}=\{an, apple, ate, I\}\), some possible sentences (not necessarily grammatically correct) are

Intuitively, some of these sentences are more probable than others.

We can think of a sentence as a sequence  \(X_1,X_2, \cdots,X_n\), where \(X_i \in \mathcal{V}\)

a. An apple ate I

b. I ate an apple 

c. I ate apple 

d. an apple 

e. .... 

What do we mean by that?

Intuitively, we mean that give a very very large corpus, we expect some of these sentences to appear more frequently than others (hence, more probable)

We are now looking for a function which takes a sequence as input and assigns a probability to each sequence

f:(X_1,X_2,\cdots X_n) \rightarrow [0,1]

Such a function is called a language model.

Language modelling

Definition

If we naively assume that  the words in a sequence are independent of each other then 

P(x_1,x_2,\cdots,x_T)=\prod \limits_{i=1}^T P(x_i)
P(x_1,x_2,\cdots,x_T)=
P(x_1)P(x_2|x_1)P(x_3|x_2,x_1) \cdots P(x_T|x_{T-1},\cdots,x_1)
=\prod \limits_{i=1}^T P(x_i|x_1,\cdots,x_{i-1})

How do we enable a model to understand language?

Simple Idea: Teach it the task of predicting the next token in a sequence..

You have tons of sequences available on the web which you can use as training data 

Roughly speaking, this task of predicting the next token in a sequence is called language modelling

?

However, we know that the words in a sentence are not independent but depend on the previous words

a. I enjoyed reading a book

b. I enjoyed reading a thermometer

The presence of "enjoyed" makes the word "book" more likely than "thermometer"

Hence, the naive assumption does not make sense

Current word \(\underbrace{x_i} \) depends on  previous words \(\underbrace{x_1,\cdots,x_{i-1}} \)

\prod \limits_{i=1}^T P(x_i|x_1,\cdots,x_{i-1}):

Current word \(\underbrace{x_i} \) depends on  previous words \(\underbrace{x_1,\cdots,x_{i-1}} \)

\prod \limits_{i=1}^T P(x_i|x_1,\cdots,x_{i-1}):

How do we estimate these conditional probabilities?

One solution: use autoregressive models where the conditional probabilities are given by parameterized functions with a fixed number of parameters (like transformers).

Causal Language Modelling (CLM)

P(x_1,x_2,\cdots,x_T)=
=P(x_1)P(x_2|x_1)P(x_3|x_2,x_1) \cdots P(x_T|x_{T-1},\cdots,x_1)
\prod \limits_{i=1}^T P(x_i|x_1,\cdots,x_{i-1})

We are looking for \(f_{\theta}\) such that

P(x_i|x_1,\cdots,x_{i-1})=f_\theta(x_i|x_1,\cdots,x_{i-1})

Can  \(f_{\theta}\) be a transformer?

Transformer

\(x_1,x_2,\cdots,x_{i-1}\)

\(P(x_i)\)

f_{\theta}

Using only the encoder of the transformer (encoder only models)

Using only the decoder of the transformer (decoder only models)

Using both the encoder and decoder of the transformer (encoder decoder models)

Multi-Head Attention

Feed forward NN

Add&Norm

Add&Norm

\(x_1,<mask>,\cdots,x_{T}\)

\(P(<mask>)\)

Multi-Head masked Attention

Feed forward NN

Add&Norm

Add&Norm

\(x_1,x_2,\cdots,x_{i-1}\)

\(P(x_i)\)

Multi-Head Attention

Feed forward NN

Add&Norm

Add&Norm

Multi-Head cross Attention

Feed forward NN

Add&Norm

Add&Norm

Multi-Head Maksed Attention

Add&Norm

\(x_1,<mask>,\cdots,x_{T}\)

\(<go>\)

\(P(<mask>)\)

Some Possibilities

Feed Forward Network

Masked Multi-Head (Self)Attention

Multi-Head (Cross) Attention

e
\langle \ go \rangle
x_1
x_2
x_3

The input is a sequence of words

We want the model to see only the present and past inputs.

We can achieve this by applying the mask.

M=\begin{bmatrix} 0&-\infty&-\infty & -\infty \\ 0&0&-\infty&-\infty\\ 0&0&0&-\infty\\ 0&0&0&0 \end{bmatrix}

The masked multi-head attention layer is required.

However, we do not need multi-head cross attention layer (as there is no encoder). 

Feed Forward Network

Masked Multi-Head (Self)Attention

p(x_1)
p(x_4|x_3,x_2,x_1)

The outputs represent each term in the chain rule

\cdots
=P(x_1)P(x_2|x_1)P(x_3|x_2,x_1) P(x_4|x_3,x_2,x_1)

However, this time the probabilities are determined by the parameters of the model,

=P(x_1;\theta)P(x_2|x_1;\theta)P(x_3|x_2,x_1;\theta) P(x_4|x_3,x_2,x_1;\theta)

Therefore, the objective is to maximize the likelihood \(L(\theta)\)

\langle go\rangle
x_1
x_2
x_3

Module 3.2 : Generative Pretrained Transformer (GPT)

Mitesh M. Khapra

AI4Bharat, Department of Computer Science and Engineering, IIT Madras

Generative Pretrained Transformer (GPT)

Now we can create a stack \((n)\) of modified decoder layers (called transformer block in the paper)

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 4

Transformer Block 5

p(x_1)
p(x_4|x_3,x_2,x_1)
\cdots
h_{l}=transformer\_block(h_{l-1}), \forall l \in [1,n]
h_{0}=X \in \mathbb{R}^{T \times d_{model}}

Let, \(X\) denote the input sequence 

h_1
h_2
h_3
h_4
h_5
P(x_i)=softmax(h_n[i]W_v)

Where \(h_n[i]\) is the \(i-\)the output vector in \(h_n\) block.

\mathscr{L}=\sum \limits_{i=1}^T \log (P(x_i|x_1,\cdots,x_{i-1}))
\langle \ go \rangle
x_1
x_2
x_3
W_v
W_v
h_{11}
h_{12}
h_{13}
h_{14}
h_{21}
h_{22}
h_{23}
h_{24}
h_{31}
h_{32}
h_{33}
h_{34}
h_{41}
h_{42}
h_{43}
h_{44}
h_{51}
h_{52}
h_{53}
h_{54}

Input data

BookCorpus

The corpus contains 7000 unique books, 74 Million sentences and approximately 1 Billion words across 16 genres

Also, uses long-range contiguous text

(i.e., no shuffling of sentences or paragraphs)

Side Note: The other benchmark dataset called 1B words could also be used. However, the sentences are not contiguous (no entailment)

Vocab size \(|\mathcal{V}|\): 40478

Tokenizer: Byte Pair Encoding

Embedding dim: \(768 \)

MODEL

Contains 12 decoder layers (transformer blocks)

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

p(x_1)
p(x_4|x_3,x_2,x_1)
\cdots
h_1
h_2
h_3
h_{12}
W_v
W_v
\vdots
\vdots
\vdots
\vdots

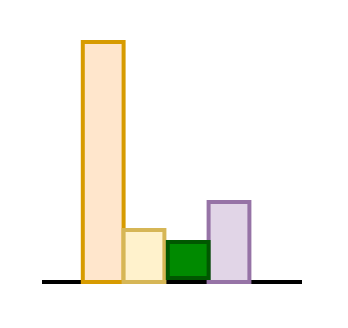
FFN hidden layer size: \(768 \times 4 = 3072\)

Attention heads: \(12 \)

Context size: \(512 \)

Dropout, layer normalization, and residual connections were implemented to enhance convergence during training.

Activation: Gaussian Error Linear Unit (GELU)

x_1
x_2
x_3
\langle \ go \rangle

Transformer Block 1

<go>

at

the

bell

labs

hamming

bound

...................

new

a

devising

..............

x_2
x_{18}
x_{351}
x_{511}

<stop>

A sample  data

Transformer Block 1

<go>

at

the

bell

labs

hamming

bound

...................

new

a

devising

..............

<stop>

Feed Forward Neural Network

Multi-head masked attention

<go>

at

the

bell

labs

hamming

bound

...................

new

a

devising

..............

<stop>

Masked Multi-head attention

Q
K
V
\text{MatMul:} \ Q^TK+M
\text{Scale}:\frac{1}{\sqrt{d_k}}
\text{Softmax}
\text{MatMul}
\text{dropout}
Q
K
V
\text{MatMul:} \ Q^TK+M
\text{Scale}:\frac{1}{\sqrt{d_k}}
\text{Softmax}
\text{MatMul}
\text{dropout}

Concatenate

Linear

Layer norm

Residual connection

\text{dropout}

<go>

at

the

bell

labs

hamming

bound

...................

new

a

devising

..............

<stop>

Masked Multi-head attention

Feed Forward Neural Network

z_1=\mathbb{R}^{768}
l={3042}
o_1=\mathbb{R}^{768}
\text{dropout}

Layer norm

Residual connection

Number of parameters

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

p(x_1)
p(x_4|x_3,x_2,x_1)
\cdots
h_1
h_2
h_3
h_{12}
W_v
W_v
\vdots
\vdots
\vdots
\vdots

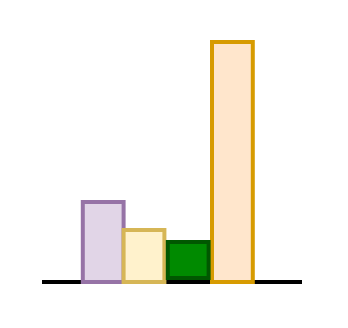
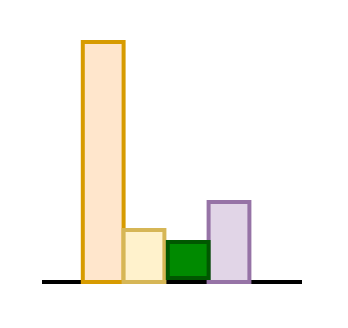
token Embeddings: \(|\mathcal{V}| \times \) embedding_dim

40478 \times 768
=31 \times 10^6
=31M

Position Embeddings : context length \(\times\) embedding_dim

Embedding Matrix

512 \times 768
=0.3 \times 10^6
=0.3M

Total: \(31.3 M\)

The positional embeddings are also learned, unlike the original transformer which uses fixed sinusoidal embeddings to encode the positions.

x_1
x_2
x_3
\langle \ go \rangle

Number of parameters

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

p(x_1)
p(x_4|x_3,x_2,x_1)
\cdots
h_1
h_2
h_3
h_{12}
W_v
W_v
\vdots
\vdots
\vdots
\vdots

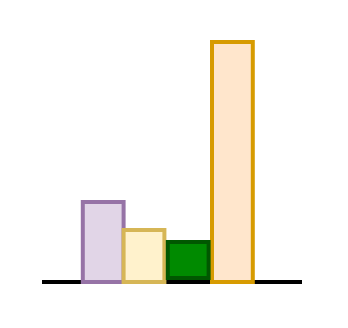
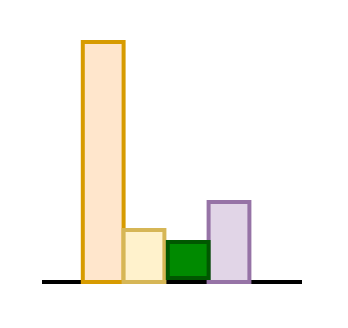
Attention parameters per block

W_Q=W_K=W_v=(768\times 64)

Per attention head

3 \times (768\times 64) \approx 147 \times 10^3

For 12 heads

12 \times 147 \times 10^3 \approx 1.7M

For a Linear layer:

768 \times 768 \approx 0.6M

For all 12 blocks

12 \times 2.3 = 27.6M
x_1
x_2
x_3
\langle \ go \rangle

Number of parameters

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

p(x_1)
p(x_4|x_3,x_2,x_1)
\cdots
h_1
h_2
h_3
h_{12}
W_v
W_v
\vdots
\vdots
\vdots
\vdots

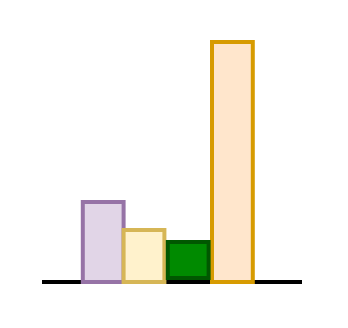
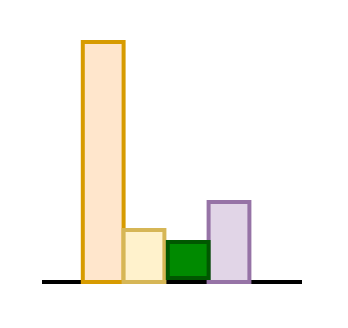
FFN parameters per block

2 \times(768 \times 3072)+3072+768 \\= 4.7 \times 10^{6}=4.7 M

For all 12 blocks

12 \times 4.7= 56.4 M
x_1
x_2
x_3
\langle \ go \rangle

Number of parameters

Transformer Block 1

Transformer Block 2

Transformer Block 3

Transformer Block 12

p(x_1)
p(x_4|x_3,x_2,x_1)
\cdots
h_1
h_2
h_3
h_{12}
W_v
W_v
\vdots
\vdots
\vdots
\vdots
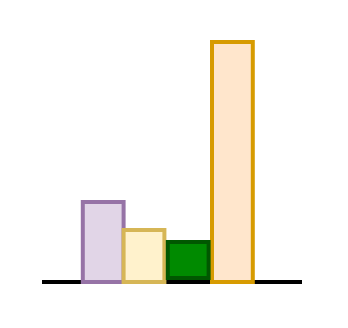
Layer Parameters (in Millions)
Embedding Layer
Attention layers
FFN Layers
Total

Embedding Matrix

31.3
27.6
56.4
116.461056^*

*Without rounding the number of parameters in each layer

Thus, GPT-1 has around 117 million parameters. 

x_1
x_2
x_3
\langle \ go \rangle

Module 3.3 : HF Transformers

Mitesh M. Khapra

AI4Bharat, Department of Computer Science and Engineering, IIT Madras

In this week

 Dataset

Encode Text

Initialize  

Model

Train the model

Decode Predictions

Tokenizer

import datasets
import tokenizers
tokenizer.encode()
tokenizer.decode()
import transformers

we will learn how to train transformer based models using the HF "transformers" module. 

Recall that we can create any architecture with a few lines of code in PyTorch

class TRANSFORMER(torch.nn.Module):
    def __init__(self,vocab_size,embed_dim,hidden_dim,num_class):
        super().__init__()
        self.embedding = nn.Embedding(vocab_size,
                                   embed_dim,
                                   padding_idx=0)
        self.transformer = nn.Transformer(dmodel,
                       nhead,
                       num_encoder_layers,
                       num_decoder_layers,
                       dim_feedforward)
        self.fc = Linear(dmodel, vocab_size)

    def forward(self, x,length)        
        x = self.embedding(x)
        x = self.transformer(x)        
        x = self.fc(x[1]) 
        return x
class RNN(torch.nn.Module):
    def __init__(self,vocab_size,embed_dim,hidden_dim,num_class):
        super().__init__()
        self.embedding = nn.Embedding(vocab_size,
                                   embed_dim,
                                   padding_idx=0)
        self.rnn = nn.RNN(embed_dim,
                       hidden_dim,
                       batch_first=True)
        self.fc = nn.Linear(hidden_dim, num_class)

    def forward(self, x,length)        
        x = self.embedding(x)
        x = pack_padded_sequence(x,
                                 lengths=length,
                                 enforce_sorted=False,
                                 batch_first=True)       
        x = self.rnn(x)        
        x = self.fc(x[1]) 
        return x
class CNN(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16 * 5 * 5, 10)
        self.fc2 = nn.Linear(10, 4)
        self.fc3 = nn.Linear(4, 2)

    def forward(self, x):

        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = x.view(-1, 16 * 5 * 5)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

We can also set up the entire training  pipeline in PyTorch

HF with PyTorch Backend

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

N samples

in a storage

data

torch.tensor

Torch.nn.module

(Linear, Transformer)

torch.optim

.Step

Training any deep learning model in PyTorch follows the sequence of operations as shown above.

torch.nn.Parameter

torch.autograd

\theta,\nabla \theta
\theta-\nabla \theta

How do we fetch the data for training the model ?

We can slice the batch and iterate, not a big deal! wait..

HF transformers module further abstracts this sequence of operations

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

N samples

in a storage

1
10
5
4
3
6
17
8
9
2
11
16
13
14
15
12
7
18

Shuffled indices

Model Under

training

Fetching the next set of batches simultaneously when the model is being trained is not possible due to python's GIL (Global Interpreter Lock)

Fetch

(Model waits until samples are fetched)

Samples may need to be randomly shuffled

The complexity of distributing data to multiple GPUs in distributed training is high.

Therefore we need a mechanism that efficiently handles all these requirements

data

The complexity becomes even greater in a multinode distributed training setup

 Dataset

Encode

 Text

Initialize  

Model

Train the model

Tokenizer

import datasets
import tokenizers
tokenizer.encode()
import transformers

Current Training Setup

 Dataset

Encode

 Text

Initialize  

Model

Train the model

Tokenizer

import datasets
import tokenizers
tokenizer.encode()
import transformers

DataLoader

Training with DataLoader

 Dataset

Initialize Model

Tokenizer

from datasets import load_dataset
from transformers import AutoTokenizer

DataLoader

The Main Sections of the Hands-on Notebook

Train the model

from transformers import DataCollatorForLanguageModeling
from transformers import GPT2Config, GPT2LMHeadModel
from transformers import TrainingArguments, Trainer

Let's dive in

HF with PyTorch Backend

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
data

torch.tensor

Torch.nn.module

(Linear, Transformer)

torch.optim

.Step

torch.nn.Parameter

torch.autograd

\theta,\nabla \theta
\theta-\nabla \theta

DLP_NLP_W3

By Arun Prakash

DLP_NLP_W3

  • 180

More from Arun Prakash